
【题目】已知函数f(x)= ![]() 若对于任意两个不等实数x1 , x2 , 都有
若对于任意两个不等实数x1 , x2 , 都有 ![]() >1成立,则实数a的取值范围是( )
>1成立,则实数a的取值范围是( )
A.[1,3)
B.[ ![]() ,3)
,3)
C.[0,4)
D.[ ![]() ,4)
,4)
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=2,CD=1,连接AC,以对角线AC为边,按逆时针方向作矩形ABCD的相似矩形AB1C1C,再连接AC1 , 以对角线AC1为边作矩形AB1C1C的相似矩形AB2C2C1 , …,按此规律继续下去,则矩形ABnCnCn﹣1的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠AOB=90°,AB∥x轴,OB=2,双曲线y=![]() 经过点B,将△AOB绕点B逆时针旋转,使点O的对应点D落在x轴的正半轴上.若AB的对应线段CB恰好经过点O.
经过点B,将△AOB绕点B逆时针旋转,使点O的对应点D落在x轴的正半轴上.若AB的对应线段CB恰好经过点O.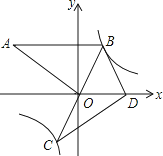
(1)求点B的坐标和双曲线的解析式;
(2)判断点C是否在双曲线上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5支篮球队进行单循环比赛(任两支球队恰进行一场比赛),任两支球队之间胜率都是 ![]() .单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.有下列四个命题:p1:恰有四支球队并列第一名为不可能事件;p2:有可能出现恰有两支球队并列第一名;p3:每支球队都既有胜又有败的概率为
.单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.有下列四个命题:p1:恰有四支球队并列第一名为不可能事件;p2:有可能出现恰有两支球队并列第一名;p3:每支球队都既有胜又有败的概率为 ![]() ;p4:五支球队成绩并列第一名的概率为
;p4:五支球队成绩并列第一名的概率为 ![]() .其中真命题是( )
.其中真命题是( )
A.p1 , p2 , p3
B.p1 , p2 , p4
C.p1 , p3 , p4
D.p2 , p3 , p4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C1:ρ2﹣4ρcosθ+3=0,θ∈[0,2π],曲线C2:ρ= ![]() ,θ∈[0,2π]. (Ⅰ)求曲线C1的一个参数方程;
,θ∈[0,2π]. (Ⅰ)求曲线C1的一个参数方程;
(Ⅱ)若曲线C1和曲线C2相交于A、B两点,求|AB|的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富人民群众业余生活,某市拟建设一座江滨公园,通过专家评审筛选出建设方案A和B向社会公开征集意见.有关部门用简单随机抽样方法调查了500名市民对这两种方案的看法,结果用条形图表示如下: 
(Ⅰ)根据已知条件完成下面的2×2列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.01的前提下认为是否选择方案A和年龄段有关?
选择方案A | 选择方案B | 总计 | |
老年人 | |||
非老年人 | |||
总计 | 500 |
附:
(Ⅱ)根据(Ⅰ)的结论,能否提出一个更好的调查方法,使得调查结果更具代表性,说明理由.
P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条抛物线y=﹣x(x﹣2)(0≤x≤2)的一部分,记为C1 , 它与x轴交于O,A1两点,将C1绕点A1旋转180°得到C2 , 交x轴于点A2 , ;将C2绕点A2旋转180°得到C3 , 交x轴于A3;…如此进行下去,直至得到C6 , 若点P(2017,y)在抛物线Cn上,则y= . 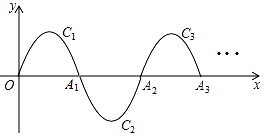
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,将△ABC绕点A顺时针旋转,使点C落在边AB上的点E处,点B落在点D处,连接BD,如果∠DAC=∠DBA,那么 ![]() 的值是 .
的值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C. 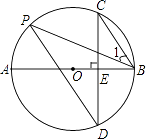
(1)求证:CB∥PD;
(2)若BC=6,sin∠P= ![]() ,求AB的值.
,求AB的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com