
【题目】在直角坐标系xOy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C1:ρ2﹣4ρcosθ+3=0,θ∈[0,2π],曲线C2:ρ= ![]() ,θ∈[0,2π]. (Ⅰ)求曲线C1的一个参数方程;
,θ∈[0,2π]. (Ⅰ)求曲线C1的一个参数方程;
(Ⅱ)若曲线C1和曲线C2相交于A、B两点,求|AB|的值.
【答案】解:(I)曲线C1:ρ2﹣4ρcosθ+3=0,θ∈[0,2π], 可得直角坐标方程:x2+y2﹣4x+3=0,配方为:(x﹣2)2+y2=1,
利用x﹣2=cosα,y=sinα,可得曲线C1的一个参数方程: ![]() (α为参数,α∈R).
(α为参数,α∈R).
(II)曲线C2:ρ=  ,(θ∈[0,2π]0,展开可得:4ρ
,(θ∈[0,2π]0,展开可得:4ρ  =3,
=3,
即2ρcosθ﹣2 ![]() sinθ=3,可得直角坐标方程:2x﹣2
sinθ=3,可得直角坐标方程:2x﹣2 ![]() y﹣3=0.
y﹣3=0.
圆心到直线l的距离d=  =
= ![]() ,∴|AB|=2
,∴|AB|=2 ![]() =2
=2 ![]() =
= ![]() .
.
【解析】(I)曲线C1:ρ2﹣4ρcosθ+3=0,θ∈[0,2π],可得直角坐标方程:x2+y2﹣4x+3=0,配方为:(x﹣2)2+y2=1,利用x﹣2=cosα,y=sinα,即可得出曲线C1的一个参数方程.(II)曲线C2:ρ= ![]() ,(θ∈[0,2π]0,展开可得:4ρ
,(θ∈[0,2π]0,展开可得:4ρ ![]() =3,即2ρcosθ﹣2
=3,即2ρcosθ﹣2 ![]() sinθ=3,把
sinθ=3,把 ![]() d代入可得直角坐标方程.利用懂得珍惜可得圆心到直线l的距离d,可得|AB|=2
d代入可得直角坐标方程.利用懂得珍惜可得圆心到直线l的距离d,可得|AB|=2 ![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】开学初,小明到文具批发部一次性购买某种笔记本,该文具批发部规定:这种笔记本售价y(元/本)与购买数量x(本)之间的函数关系如图所示.
(1)图中线段AB所表示的实际意义是;
(2)请直接写出y与x之间的函数关系式;
(3)已知该文具批发部这种笔记本的进价是3元/本,若小明购买此种笔记本超过10本但不超过20本,那么小明购买多少本时,该文具批发部在这次买卖中所获的利润W(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,对角线AC与BD交于点O;在Rt△PMN中,∠MPN=90°.
(1)如图1,若点P与点O重合且PM⊥AD、PN⊥AB,分别交AD、AB于点E、F,请直接写出PE与PF的数量关系;
(2)将图1中的Rt△PMN绕点O顺时针旋转角度α(0°<α<45°).
①如图2,在旋转过程中(1)中的结论依然成立吗?若成立,请证明;若不成立,请说明理由;
②如图2,在旋转过程中,当∠DOM=15°时,连接EF,若正方形的边长为2,请直接写出线段EF的长;
③如图3,旋转后,若Rt△PMN的顶点P在线段OB上移动(不与点O、B重合),当BD=3BP时,猜想此时PE与PF的数量关系,并给出证明;当BD=mBP时,请直接写出PE与PF的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣a|+|2x﹣1|,a∈R. (I)当a=3时,求关于x的不等式f(x)≤6的解集;
(II)当x∈R时,f(x)≥a2﹣a﹣13,求实数a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数列{an}中,a1=1,an+1=(n+1)an+(n+1)!. (Ⅰ)求证:数列 ![]() 是等差数列,并求{an}的通项公式;
是等差数列,并求{an}的通项公式;
(Ⅱ)求{an}的前n项和Sn .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 若对于任意两个不等实数x1 , x2 , 都有
若对于任意两个不等实数x1 , x2 , 都有 ![]() >1成立,则实数a的取值范围是( )
>1成立,则实数a的取值范围是( )
A.[1,3)
B.[ ![]() ,3)
,3)
C.[0,4)
D.[ ![]() ,4)
,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)=mex+x+1. (Ⅰ)讨论f(x)的单调性;
(Ⅱ)若f(x)有两个零点x1 , x2(x1<x2),证明:x1+x2>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c过点B(3,0),C(0,3),D为抛物线的顶点.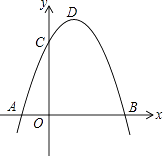
(1)求抛物线的解析式以及顶点坐标;
(2)点C关于抛物线y=﹣x2+bx+c对称轴的对称点为E点,联结BC,BE,求∠CBE的正切值;
(3)点M是抛物线对称轴上一点,且△DMB和△BCE相似,求点M坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,Rt△ABC中,∠ACB=90°,BC=8,cot∠BAC= ![]() ,点D在边BC上(不与点B、C重合),点E在边BC的延长线上,∠DAE=∠BAC,点F在线段AE上,∠ACF=∠B.设BD=x.
,点D在边BC上(不与点B、C重合),点E在边BC的延长线上,∠DAE=∠BAC,点F在线段AE上,∠ACF=∠B.设BD=x.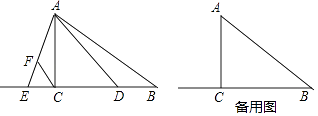
(1)若点F恰好是AE的中点,求线段BD的长;
(2)若y= ![]() ,求y关于x的函数关系式,并写出它的定义域;
,求y关于x的函数关系式,并写出它的定义域;
(3)当△ADE是以AD为腰的等腰三角形时,求线段BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com