
【题目】已知函数f(x)=|2x﹣a|+|2x﹣1|,a∈R. (I)当a=3时,求关于x的不等式f(x)≤6的解集;
(II)当x∈R时,f(x)≥a2﹣a﹣13,求实数a的取值范围.
【答案】解:(I)当a=3时,不等式f(x)≤6为|2x﹣3|+|2x﹣1|≤6 若 ![]() 时,不等式可化为﹣(2x﹣3)﹣(2x﹣1)=﹣4x+4≤6,解得
时,不等式可化为﹣(2x﹣3)﹣(2x﹣1)=﹣4x+4≤6,解得 ![]() ,
,
若 ![]() 时,不等式可化为﹣(2x﹣3)+(2x﹣1)=2≤6,解得
时,不等式可化为﹣(2x﹣3)+(2x﹣1)=2≤6,解得 ![]() ,
,
若 ![]() 时,不等式可化为(2x﹣3)+(2x﹣1)=4x﹣4≤6,解得
时,不等式可化为(2x﹣3)+(2x﹣1)=4x﹣4≤6,解得 ![]() ,
,
综上所述,关于x的不等式f(x)≤6的解集为 ![]() . …
. …
(II)当x∈R时,f(x)=|2x﹣a|+|2x﹣1|≥|2x﹣a+1﹣2x|=|1﹣a|,
所以当x∈R时,f(x)≥a2﹣a﹣13等价于|1﹣a|≥a2﹣a﹣13,
当a≤1时,等价于1﹣a≥a2﹣a﹣13,解得 ![]() ,
,
当a>1时,等价于a﹣1≥a2﹣a﹣13,解得 ![]() ,
,
所以a的取值范围为 ![]() .
.
【解析】(I)分类讨论,即可求关于x的不等式f(x)≤6的解集;(II)当x∈R时,f(x)≥a2﹣a﹣13等价于|1﹣a|≥a2﹣a﹣13,分类讨论,求实数a的取值范围.
【考点精析】通过灵活运用绝对值不等式的解法,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,直线y=ax+1与x轴、y轴分别相交于A、B两点,与双曲线y= ![]() (x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(1)求双曲线的解析式;
(2)若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角形与△AOB相似时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形,E为BC边中点,连接AE,以AD为直径的⊙O交AE于点F,连接CF.
(1)求证:CF与⊙O相切;
(2)若AD=2,F为AE的中点,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠AOB=90°,AB∥x轴,OB=2,双曲线y=![]() 经过点B,将△AOB绕点B逆时针旋转,使点O的对应点D落在x轴的正半轴上.若AB的对应线段CB恰好经过点O.
经过点B,将△AOB绕点B逆时针旋转,使点O的对应点D落在x轴的正半轴上.若AB的对应线段CB恰好经过点O.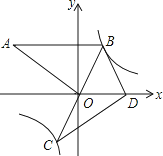
(1)求点B的坐标和双曲线的解析式;
(2)判断点C是否在双曲线上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了引导居民合理用水,居民生活用水实行二级阶梯水价计量办法,具体如下:第一阶梯,每户居民月用水量不超过12吨,价格为4元/吨;第二阶梯,每户居民月用水量超过12吨,超过部分的价格为8元/吨.为了了解全市居民月用水量的分布情况,通过抽样获得了100户居民的月用水量(单位:吨),将数据按照[0,2],(2,4],…,(14,16]分成8组,制成了如图1所示的频率分布直方图. 
(Ⅰ)求频率分布直方图中字母a的值,并求该组的频率;
(Ⅱ)通过频率分布直方图,估计该市居民每月的用水量的中位数m的值(保留两位小数);
(Ⅲ)如图2是该市居民张某2016年1~6月份的月用水费y(元)与月份x的散点图,其拟合的线性回归方程是 ![]() =2x+33,若张某2016年1~7月份水费总支出为312元,试估计张某7月份的用水吨数.
=2x+33,若张某2016年1~7月份水费总支出为312元,试估计张某7月份的用水吨数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5支篮球队进行单循环比赛(任两支球队恰进行一场比赛),任两支球队之间胜率都是 ![]() .单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.有下列四个命题:p1:恰有四支球队并列第一名为不可能事件;p2:有可能出现恰有两支球队并列第一名;p3:每支球队都既有胜又有败的概率为
.单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.有下列四个命题:p1:恰有四支球队并列第一名为不可能事件;p2:有可能出现恰有两支球队并列第一名;p3:每支球队都既有胜又有败的概率为 ![]() ;p4:五支球队成绩并列第一名的概率为
;p4:五支球队成绩并列第一名的概率为 ![]() .其中真命题是( )
.其中真命题是( )
A.p1 , p2 , p3
B.p1 , p2 , p4
C.p1 , p3 , p4
D.p2 , p3 , p4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C1:ρ2﹣4ρcosθ+3=0,θ∈[0,2π],曲线C2:ρ= ![]() ,θ∈[0,2π]. (Ⅰ)求曲线C1的一个参数方程;
,θ∈[0,2π]. (Ⅰ)求曲线C1的一个参数方程;
(Ⅱ)若曲线C1和曲线C2相交于A、B两点,求|AB|的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条抛物线y=﹣x(x﹣2)(0≤x≤2)的一部分,记为C1 , 它与x轴交于O,A1两点,将C1绕点A1旋转180°得到C2 , 交x轴于点A2 , ;将C2绕点A2旋转180°得到C3 , 交x轴于A3;…如此进行下去,直至得到C6 , 若点P(2017,y)在抛物线Cn上,则y= . 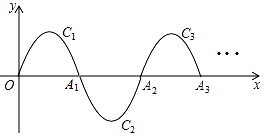
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,第一象限内的点A,B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且cot∠ACB= ![]()

求:
(1)反比例函数的解析式;
(2)点C的坐标;
(3)∠ABC的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com