
【题目】某市为了引导居民合理用水,居民生活用水实行二级阶梯水价计量办法,具体如下:第一阶梯,每户居民月用水量不超过12吨,价格为4元/吨;第二阶梯,每户居民月用水量超过12吨,超过部分的价格为8元/吨.为了了解全市居民月用水量的分布情况,通过抽样获得了100户居民的月用水量(单位:吨),将数据按照[0,2],(2,4],…,(14,16]分成8组,制成了如图1所示的频率分布直方图. 
(Ⅰ)求频率分布直方图中字母a的值,并求该组的频率;
(Ⅱ)通过频率分布直方图,估计该市居民每月的用水量的中位数m的值(保留两位小数);
(Ⅲ)如图2是该市居民张某2016年1~6月份的月用水费y(元)与月份x的散点图,其拟合的线性回归方程是 ![]() =2x+33,若张某2016年1~7月份水费总支出为312元,试估计张某7月份的用水吨数.
=2x+33,若张某2016年1~7月份水费总支出为312元,试估计张某7月份的用水吨数.
【答案】解:(Ⅰ)∵(0.02+0.04+0.08+a+0.13+0.03+0.02)×2=1, ∴a=0.10,
第四组的频率为0.1×2=0.2,
(Ⅱ)∵0.02×2+0.04×2+0.08×2+0.10×2+(m﹣8)×0.13=0.5
∴m=8+ ![]() ≈8.15.
≈8.15.
(Ⅲ)∵ ![]() =
= ![]() (1+2+3+4+5+6)=
(1+2+3+4+5+6)= ![]() ,且
,且 ![]() =2x+33,
=2x+33,
∴ ![]() =2×
=2× ![]() +33=40,
+33=40,
∴所以张某7月份的水费为312﹣6×40=72,
设张某7月份的用水吨数为x吨,
∵12×4=48<72,
∴12×4+(x﹣12)×8=72,
解得x=15,
则张某7月份的用水吨数为15吨
【解析】(Ⅰ)根据小长方形的面积之和为1,即可求出a,(Ⅱ)由频率分布直方图估计样本数据的中位数,规律是:中位数,出现在概率是0.5的地方,(Ⅲ)根据回归方程即可求出答案
【考点精析】本题主要考查了频率分布直方图的相关知识点,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息才能正确解答此题.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC,D是边BC的中点,过D作DE∥AB于E,连接BE交AD于D1;过D1作D1E1∥AB于E1 , 连接BE1交AD于D2;过D2作D2E2∥AB于E2 , …,如此继续,若记S△BDE为S1 , 记 ![]() 为S2 , 记
为S2 , 记 ![]() 为S3…,若S△ABC面积为Scm,则Sn=cm(用含n与S的代数式表示)
为S3…,若S△ABC面积为Scm,则Sn=cm(用含n与S的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1 , 使AA1=BB1=CC1=DD1=![]() a,在边A1B1、B1C1、C1D1、D1A1上分别取点A2、B2、C2、D2 , 使A1A2=B1B2=C1C2=D1D2=
a,在边A1B1、B1C1、C1D1、D1A1上分别取点A2、B2、C2、D2 , 使A1A2=B1B2=C1C2=D1D2=![]() A1B2 , ….依次规律继续下去,则正方形AnBnCnDn的面积为 .
A1B2 , ….依次规律继续下去,则正方形AnBnCnDn的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,对角线AC与BD交于点O;在Rt△PMN中,∠MPN=90°.
(1)如图1,若点P与点O重合且PM⊥AD、PN⊥AB,分别交AD、AB于点E、F,请直接写出PE与PF的数量关系;
(2)将图1中的Rt△PMN绕点O顺时针旋转角度α(0°<α<45°).
①如图2,在旋转过程中(1)中的结论依然成立吗?若成立,请证明;若不成立,请说明理由;
②如图2,在旋转过程中,当∠DOM=15°时,连接EF,若正方形的边长为2,请直接写出线段EF的长;
③如图3,旋转后,若Rt△PMN的顶点P在线段OB上移动(不与点O、B重合),当BD=3BP时,猜想此时PE与PF的数量关系,并给出证明;当BD=mBP时,请直接写出PE与PF的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠C=90°,点D在AC上,且CD>DA,DA=2,点P,Q同时从点D出发,以相同的速度分别沿射线DC、射线DA运动,过点Q作AC的垂线段QR,使QR=PQ,连接PR,当点Q到达点A时,点P,Q同时停止运动.设PQ=x,△PQR与△ABC重叠部分的面积为S,S关于x的函数图象如图2所示(其中0<x≤![]() ,
, ![]() <x≤m时,函数的解析式不同).
<x≤m时,函数的解析式不同).
(1)填空:n的值为___;
(2)求S关于x的函数关系式,并写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣a|+|2x﹣1|,a∈R. (I)当a=3时,求关于x的不等式f(x)≤6的解集;
(II)当x∈R时,f(x)≥a2﹣a﹣13,求实数a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数列{an}中,a1=1,an+1=(n+1)an+(n+1)!. (Ⅰ)求证:数列 ![]() 是等差数列,并求{an}的通项公式;
是等差数列,并求{an}的通项公式;
(Ⅱ)求{an}的前n项和Sn .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)=mex+x+1. (Ⅰ)讨论f(x)的单调性;
(Ⅱ)若f(x)有两个零点x1 , x2(x1<x2),证明:x1+x2>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=1.5米,BE=2.3米,求拉线CE的长,(精确到0.1米)参考数据 ![]() ≈1.41,
≈1.41, ![]() ≈1.73.
≈1.73. 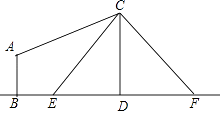
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com