
【题目】已知函数f(x)=mex+x+1. (Ⅰ)讨论f(x)的单调性;
(Ⅱ)若f(x)有两个零点x1 , x2(x1<x2),证明:x1+x2>0.
【答案】(Ⅰ)解:f′(x)=mex+1, m≥0时,f′(x)>0,f(x)在R递增,
m<0时,令f′(x)>0,解得:x<ln(﹣ ![]() ),
),
令f′(x)<0,解得:x>ln(﹣ ![]() ),
),
故f(x)在(﹣∞,ln(﹣ ![]() ))递增,在(ln(﹣
))递增,在(ln(﹣ ![]() ),+∞)递减;
),+∞)递减;
(Ⅱ)证明:若f(x)有两个零点x1 , x2(x1<x2),
由(Ⅰ)得:f(x)max=f(ln(﹣ ![]() ))=ln(﹣
))=ln(﹣ ![]() )>0,
)>0,
解得:﹣1<m<0,
由f(x1)=f(x2)得:m= ![]() ①,
①,
m( ![]() ﹣
﹣ ![]() )+(x1﹣x2)=0②,
)+(x1﹣x2)=0②,
将①代入②整理得:
x1= ![]() +1,
+1,
故x2+x1= ![]() +1+x2 ,
+1+x2 ,
由m= ![]() =
= ![]() 得:﹣1<
得:﹣1< ![]() <0,
<0,
解得:﹣1<x2<0,
令g(x)= ![]() +x+1,(﹣1<x<0),
+x+1,(﹣1<x<0),
则g′(x)=1﹣xe﹣x>0,
故g(x)在(﹣1,0)递增,
g(x)>g(﹣1)=0,
故x2+x1= ![]() +1+x2>0.
+1+x2>0.
【解析】(Ⅰ)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;(Ⅱ)求出x2+x1= ![]() +1+x2 , 由m=
+1+x2 , 由m= ![]() =
= ![]() ,解得:﹣1<x2<0,令g(x)=
,解得:﹣1<x2<0,令g(x)= ![]() +x+1,(﹣1<x<0),根据函数的单调性证明即可.
+x+1,(﹣1<x<0),根据函数的单调性证明即可.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+
x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+![]() x+c经过B、C两点.
x+c经过B、C两点.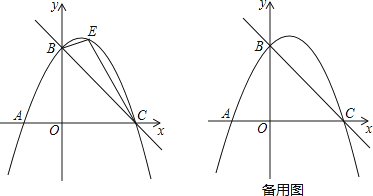
(1)求抛物线的解析式;
(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标和△BEC面积的最大值?
(3)在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了引导居民合理用水,居民生活用水实行二级阶梯水价计量办法,具体如下:第一阶梯,每户居民月用水量不超过12吨,价格为4元/吨;第二阶梯,每户居民月用水量超过12吨,超过部分的价格为8元/吨.为了了解全市居民月用水量的分布情况,通过抽样获得了100户居民的月用水量(单位:吨),将数据按照[0,2],(2,4],…,(14,16]分成8组,制成了如图1所示的频率分布直方图. 
(Ⅰ)求频率分布直方图中字母a的值,并求该组的频率;
(Ⅱ)通过频率分布直方图,估计该市居民每月的用水量的中位数m的值(保留两位小数);
(Ⅲ)如图2是该市居民张某2016年1~6月份的月用水费y(元)与月份x的散点图,其拟合的线性回归方程是 ![]() =2x+33,若张某2016年1~7月份水费总支出为312元,试估计张某7月份的用水吨数.
=2x+33,若张某2016年1~7月份水费总支出为312元,试估计张某7月份的用水吨数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C1:ρ2﹣4ρcosθ+3=0,θ∈[0,2π],曲线C2:ρ= ![]() ,θ∈[0,2π]. (Ⅰ)求曲线C1的一个参数方程;
,θ∈[0,2π]. (Ⅰ)求曲线C1的一个参数方程;
(Ⅱ)若曲线C1和曲线C2相交于A、B两点,求|AB|的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条抛物线y=﹣x(x﹣2)(0≤x≤2)的一部分,记为C1 , 它与x轴交于O,A1两点,将C1绕点A1旋转180°得到C2 , 交x轴于点A2 , ;将C2绕点A2旋转180°得到C3 , 交x轴于A3;…如此进行下去,直至得到C6 , 若点P(2017,y)在抛物线Cn上,则y= . 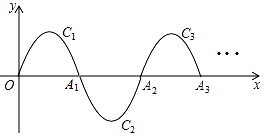
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,cosA= ![]() ,BE,CF分别是AC,AB边上的高,联结EF,那么△AEF和△ABC的周长比为( )
,BE,CF分别是AC,AB边上的高,联结EF,那么△AEF和△ABC的周长比为( ) 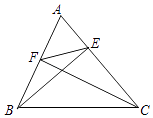
A.1:2
B.1:3
C.1:4
D.1:9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE∥BC,且过△ABC的重心,分别与AB,AC交于点D,E,点P是线段DE上一点,CP的延长线交AB于点Q,如果 ![]() =
= ![]() ,那么S△DPQ:S△CPE的值是 .
,那么S△DPQ:S△CPE的值是 . 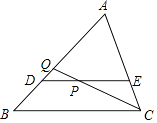
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,⊙A切y轴于点B,且点A在反比例函数y= ![]() (x>0)的图象上,连接OA交⊙A于点C,且点C为OA中点,则图中阴影部分的面积为( )
(x>0)的图象上,连接OA交⊙A于点C,且点C为OA中点,则图中阴影部分的面积为( ) 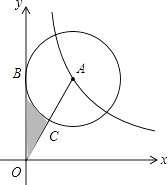
A.4 ![]() ﹣
﹣ ![]()
B.4 ![]()
C.2 ![]()
D.2 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com