
����Ŀ����ͼ��ֱ��y=![]() x+3��x�ύ�ڵ�C����y�ύ�ڵ�B��������y=ax2+
x+3��x�ύ�ڵ�C����y�ύ�ڵ�B��������y=ax2+![]() x+c����B��C���㣮
x+c����B��C���㣮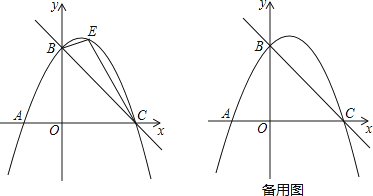
��1���������ߵĽ���ʽ��
��2����ͼ����E��ֱ��BC�Ϸ��������ϵ�һ���㣬����BEC������ʱ���������E������͡�BEC��������ֵ��
��3���ڣ�2���Ľ����£�����E��y���ƽ���߽�ֱ��BC�ڵ�M������AM����Q�������߶Գ����ϵĶ��㣬�����������Ƿ���ڵ�P��ʹ����P��Q��A��MΪ������ı�����ƽ���ı��Σ�������ڣ���ֱ��д����P�����ꣻ��������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��ֱ��y=![]() x+3��x�ύ�ڵ�C����y�ύ�ڵ�B��
x+3��x�ύ�ڵ�C����y�ύ�ڵ�B��
���B�������ǣ�0��3������C�������ǣ�4��0����
��������y=ax2+![]() x+c����B��C���㣬
x+c����B��C���㣬
��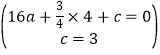
���
��y=![]() .
.
��2��
�⣺��ͼ1������E��y���ƽ����EF��ֱ��BC�ڵ�M��EF��x���ڵ�F��
 ��
��
�ߵ�E��ֱ��BC�Ϸ��������ϵ�һ���㣬
�����E�������ǣ�x��![]() ����
����
���M�������ǣ�x��![]() x+3����
x+3����
��EM=![]() ����
����![]() +3��=
+3��=![]() x2+
x2+![]() x��
x��
��S��BEC=S��BEM+S��MEC
=![]()
=![]() ����
����![]() ����4
����4
=![]() x2+3x
x2+3x
=![]() ��x��2��2+3��
��x��2��2+3��
�൱x=2ʱ������E�������ǣ�2��3��ʱ����BEC����������������3��
��3��
�⣺���������ϴ��ڵ�P��ʹ����P��Q��A��MΪ������ı�����ƽ���ı��Σ�
����ͼ2��
 ��
��
�ɣ�2�����ɵõ�M�ĺ�������2��
�ߵ�M��ֱ��y=![]() x+3�ϣ�
x+3�ϣ�
���M�������ǣ�2��![]() ����
����
�֡ߵ�A�������ǣ���2��0����
��AM=![]() =
= ![]() ��
��
��AM���ڵ�ֱ�ߵ�б���ǣ�![]() =
=![]() ��
��
��y=![]() x2+
x2+ ![]() x+3�ĶԳ�����x=1��
x+3�ĶԳ�����x=1��
�����Q�������ǣ�1��m������P�������ǣ�x��![]() x2+
x2+ ![]() x+3������:
x+3������:

��� ��
��
��x��0��
���P�������ǣ���3��![]() ����
����
����ͼ3��
 ��
��
�ɣ�2�����ɵõ�M�ĺ�������2��
�ߵ�M��ֱ��y=![]() x+3�ϣ�
x+3�ϣ�
���M�������ǣ�2�� ![]() ����
����
�֡ߵ�A�������ǣ���2��0����
��AM=![]() =
= ![]() ��
��
��AM���ڵ�ֱ�ߵ�б���ǣ� ![]() =
=![]() ��
��
��y=![]() x2+
x2+ ![]() x+3�ĶԳ�����x=1��
x+3�ĶԳ�����x=1��
�����Q�������ǣ�1��m������P�������ǣ�x��![]() x2+
x2+ ![]() x+3������:
x+3������:
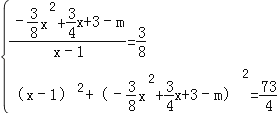
��� ��
��
��x��0��
���P�������ǣ�5��![]() ����
����
����ͼ4��
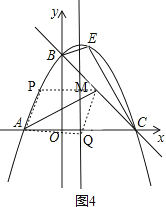 ��
��
�ɣ�2�����ɵõ�M�ĺ�������2��
�ߵ�M��ֱ��y=![]() x+3�ϣ�
x+3�ϣ�
���M�������ǣ�2�� ![]() ����
����
�֡ߵ�A�������ǣ���2��0����
��AM=![]() =
= ![]() ��
��
��AM���ڵ�ֱ�ߵ�б���ǣ� ![]() =
=![]() ��
��
��y=![]() x2+
x2+ ![]() x+3�ĶԳ�����x=1��
x+3�ĶԳ�����x=1��
�����Q�������ǣ�1��m������P�������ǣ�x��![]() x2+
x2+ ![]() x+3������:
x+3������:

���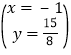
���P�������ǣ���1�� ![]() ����
����
���ϣ��ɵ�
���������ϴ��ڵ�P��ʹ����P��Q��A��MΪ������ı�����ƽ���ı��Σ�
��P�������ǣ���3��![]() ������5��
������5��![]() ��������1��
��������1�� ![]() ����
����
����������1�����ȸ���ֱ��y=��![]() x+3��x�ύ�ڵ�C����y�ύ�ڵ�B�������B�������ǣ�0��3������C�������ǣ�4��0����Ȼ�����������y=ax2+
x+3��x�ύ�ڵ�C����y�ύ�ڵ�B�������B�������ǣ�0��3������C�������ǣ�4��0����Ȼ�����������y=ax2+![]() x+c����B��C���㣬���a\c��ֵ�Ƕ��٣�������������ߵĽ���ʽ��
x+c����B��C���㣬���a\c��ֵ�Ƕ��٣�������������ߵĽ���ʽ��
��2�����ȹ���E��y���ƽ����EF��ֱ��BC�ڵ�M��EF��x���ڵ�F��Ȼ�����E�������ǣ�x����![]() x2+
x2+![]() x+3�������M�������ǣ�x����
x+3�������M�������ǣ�x����![]() x+3�������EM��ֵ�Ƕ��٣������������ε�����������S��ABC �� �����жϳ�����BEC������ʱ����E������͡�BEC��������ֵ���Ƕ��ټ��ɣ�
x+3�������EM��ֵ�Ƕ��٣������������ε�����������S��ABC �� �����жϳ�����BEC������ʱ����E������͡�BEC��������ֵ���Ƕ��ټ��ɣ�
��3�����������ϴ��ڵ�P��ʹ����P��Q��A��MΪ������ı�����ƽ���ı��Σ�Ȼ�������������ۣ�����ƽ���ı��ε����������ʹ����P��Q��A��MΪ������ı�����ƽ���ı��εĵ�P�������Ƕ��ټ��ɣ�
�����㾫�������ö��κ�������ֵ����Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪����Ա�����ȡֵ��Χ��ȫ��ʵ������ô�����ڶ��㴦ȡ�����ֵ������Сֵ��������x=-b/2aʱ��y��ֵ=(4ac-b2)/4a��


 ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���D�DZ�AB��һ�㣬��E�DZ�AC��һ�㣬��DE��BC����B=40�㣬��AED=60�㣬���A�Ķ����ǣ�������
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ȱߡ�ABC��D�DZ�BC���е㣬��D��DE��AB��E������BE��AD��D1����D1��D1E1��AB��E1 �� ����BE1��AD��D2����D2��D2E2��AB��E2 �� ������˼���������S��BDEΪS1 �� �� ![]() ΪS2 �� ��
ΪS2 �� �� ![]() ΪS3������S��ABC���ΪScm����Sn=cm���ú�n��S�Ĵ���ʽ��ʾ��
ΪS3������S��ABC���ΪScm����Sn=cm���ú�n��S�Ĵ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ����С�����ľ�������һ���Թ���ij�ֱʼDZ������ľ��������涨�����ֱʼDZ��ۼ�y��Ԫ/�����빺������x������֮��ĺ�����ϵ��ͼ��ʾ��
��1��ͼ���߶�AB����ʾ��ʵ����������
��2����ֱ��д��y��x֮��ĺ�����ϵʽ��
��3����֪���ľ����������ֱʼDZ��Ľ�����3Ԫ/������С��������ֱʼDZ�����10����������20������ôС��������ٱ�ʱ�����ľ���������������������������W��Ԫ�������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С��A�ڸۿ�B�ı�ƫ��50�㷽��С��C�ڸۿ�B�ı�ƫ��25�㷽��һ���ִ���ÿСʱ20������ٶȴӸۿ�B������С��A���У�����5Сʱ����С��A����ʱ���С��C��С��A�ı�ƫ��70�㷽����С��A����С��C�ж��ٺ�����������ȷ��1����ο����ݣ�![]() ��1.1414��
��1.1414��![]() ��1.732��
��1.732��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ������ѧ�����Ķ�ϰ�ߣ�ijУ��չ�ˡ������飬���ɳ���ϵ�л����������һ��ͼ�飬����ǰ����ѧ��ϲ���Ķ���ͼ�����ͽ����˳������飬�����������ݻ��Ƴ�������������ͳ��ͼ����ͼ��ʾ������ͳ��ͼ���ṩ����Ϣ���ش��������⣺
��1�����ε��鹲�������ѧ��������ͳ��ͼ�е�m= �� n= ��
��2����֪��У����960��ѧ��������Ƹ�Уϲ���Ķ���A����ͼ���ѧ��Լ�ж����ˣ�
��3��ѧУҪ�ٰ����֪ʶ���������꣨1����Ҫ�ڰ༶��ʤ��2��1Ů�����ѡ��2�˲�������ѡ�͵���������ͬѧΪ1��1Ů�ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊa����AB��BC��CD��DA���Ϸֱ�ȡ��A1��B1��C1��D1 �� ʹAA1=BB1=CC1=DD1=![]() a���ڱ�A1B1��B1C1��C1D1��D1A1�Ϸֱ�ȡ��A2��B2��C2��D2 �� ʹA1A2=B1B2=C1C2=D1D2=
a���ڱ�A1B1��B1C1��C1D1��D1A1�Ϸֱ�ȡ��A2��B2��C2��D2 �� ʹA1A2=B1B2=C1C2=D1D2=![]() A1B2 �� �������ι��ɼ�����ȥ����������AnBnCnDn�����Ϊ .
A1B2 �� �������ι��ɼ�����ȥ����������AnBnCnDn�����Ϊ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABCD�У��Խ���AC��BD���ڵ�O����Rt��PMN�У���MPN=90�㣮
��1����ͼ1������P���O�غ���PM��AD��PN��AB���ֱ�AD��AB�ڵ�E��F����ֱ��д��PE��PF��������ϵ��
��2����ͼ1�е�Rt��PMN�Ƶ�O˳ʱ����ת�ǶȦ���0�㣼����45�㣩��
����ͼ2������ת�����У�1���еĽ�����Ȼ����������������֤����������������˵�����ɣ�
����ͼ2������ת�����У�����DOM=15��ʱ������EF���������εı߳�Ϊ2����ֱ��д���߶�EF�ij���
����ͼ3����ת����Rt��PMN�Ķ���P���߶�OB���ƶ��������O��B�غϣ�����BD=3BPʱ�������ʱPE��PF��������ϵ��������֤������BD=mBPʱ����ֱ��д��PE��PF��������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=mex+x+1�� ��������f��x���ĵ����ԣ�
������f��x�����������x1 �� x2��x1��x2����֤����x1+x2��0��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com