
【题目】如图,小岛A在港口B的北偏东50°方向,小岛C在港口B的北偏西25°方向,一艘轮船以每小时20海里的速度从港口B出发向小岛A航行,经过5小时到达小岛A,这时测得小岛C在小岛A的北偏西70°方向,求小岛A距离小岛C有多少海里?(最后结果精确到1海里,参考数据:![]() ≈1.1414,
≈1.1414,![]() ≈1.732)
≈1.732)
【答案】解:由题意得,∠ABC=25°+50°=75°,∠BAC=180°﹣70°﹣50°=60°,
∴在△ABC中,∠C=45°,
过点B作BD⊥AC,垂足为点D,
∵AB=20×5=100,
在Rt△ABD中,∠BAD=60°,
∴BD=ABsin60°=100×![]() =
=![]() ,
,
∴AD=ABcos60°=100×![]() =50,
=50,
在Rt△BCD中,∠C=45°,
∴CD=BD=![]() ,
,
∴AC=AD+CD=50+![]() ≈137(海里),
≈137(海里),
答:小岛A距离小岛C约是137海里.
【解析】过点B作BD⊥AC,垂足为点D,根据题意求出∠ABC和∠BAC的度数以及AB的长,再求出AD和BD的长,结合CD=BD,即可求出AC的长.
【考点精析】根据题目的已知条件,利用关于方向角问题的相关知识可以得到问题的答案,需要掌握指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD是BC边上的中线,以AD为直径作⊙O,连接BO并延长至E,使得OE=OB,连接AE.
(1)求证:AE是⊙O的切线;
(2)若BD=![]() AD=4,求阴影部分的面积.
AD=4,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在第一象限,⊙A与x轴交于B(2,0)、C(8,0)两点,与y轴相切于点D,则点A的坐标是( )
A.(5,4)
B.(4,5)
C.(5,3)
D.(3,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年5月,某校组织了以“德润书香”为主题的电子小报制作比赛,评分结果只有60,70,80,90,100五种,现从中随机抽取部分作品,对其份数和成绩进行整理,制成如下两幅不完整的统计图:
根据以上信息,解答下列问题:
(1)求本次抽取了多少份作品,并补全两幅统计图;
(2)已知该校收到参赛作品共900份,比赛成绩达到90分以上(含90分)的为优秀作品,据此估计该校参赛作品中,优秀作品有多少份?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+2经过点A(﹣1,0)和点B(4,0),且与y轴交于点C,点D的坐标为(2,0),点P(m,n)是该抛物线上的一个动点,连接CA,CD,PD,PB.
(1)求该抛物线的解析式;
(2)当△PDB的面积等于△CAD的面积时,求点P的坐标;
(3)当m>0,n>0时,过点P作直线PE⊥y轴于点E交直线BC于点F,过点F作FG⊥x轴于点G,连接EG,请直接写出随着点P的运动,线段EG的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+
x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+![]() x+c经过B、C两点.
x+c经过B、C两点.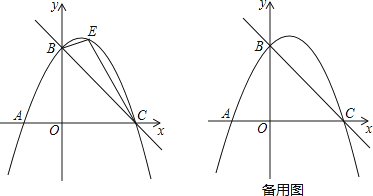
(1)求抛物线的解析式;
(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标和△BEC面积的最大值?
(3)在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.
(1)如图a,求证:△BCP≌△DCQ;
(2)如图,延长BP交直线DQ于点E.
①如图b,求证:BE⊥DQ;
②如图c,若△BCP为等边三角形,判断△DEP的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲市到乙市乘坐高速列车的路程为180千米,乘坐普通列车的路程为240千米.高速列车的平均速度是普通列车的平均速度的3倍.高速列车的乘车时间比普通列车的乘车时间缩短了2小时.高速列车的平均速度是每小时多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com