
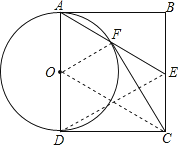
【题目】如图,四边形ABCD为矩形,E为BC边中点,连接AE,以AD为直径的⊙O交AE于点F,连接CF.
(1)求证:CF与⊙O相切;
(2)若AD=2,F为AE的中点,求AB的长.
【答案】
(1)
证明:如图所示:连接OF、OC,
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,∠ADC=90°,
∵E为BC边中点,AO=DO,
∴AO=![]() AD,EC=
AD,EC=![]() BC,
BC,
∴AO=EC,AO∥EC,
∴四边形OAEC是平行四边形,
∴AE∥OC,
∴∠DOC=∠OAF,∠FOC=∠OFA,
∵OA=OF,
∴∠OAF=∠OFA,
∴∠DOC=∠FOC,
∵在△ODC和△OFC中
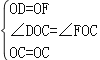 ,
,
∴△ODC≌△OFC(SAS),
∴∠OFC=∠ODC=90°,
∴OF⊥CF,
∴CF与⊙O相切;
(2)
解:如图所示:连接DE,
∵AO=DO,AF=EF,AD=2,
∴DE=20F=2,
∵E是BC的中点,
∴EC=1,
在Rt△DCE中,由勾股定理得:
DC=![]() ,
,
∴AB=CD=![]() .
.
【解析】(1)利用平行四边形的判定方法得出四边形OAEC是平行四边形,进而得出△ODC≌△OFC(SAS),求出OF⊥CF,进而得出答案;
(2)利用勾股定理得出DC的长,即可得出AB的长,
【考点精析】本题主要考查了勾股定理的概念和矩形的性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;矩形的四个角都是直角,矩形的对角线相等才能正确解答此题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等腰△OBC的边OB在x轴上,OB=CB,OB边上的高CA与OC边上的高BE相交于点D,连接OD,AB=![]() ,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是 .
,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开学初,小明到文具批发部一次性购买某种笔记本,该文具批发部规定:这种笔记本售价y(元/本)与购买数量x(本)之间的函数关系如图所示.
(1)图中线段AB所表示的实际意义是;
(2)请直接写出y与x之间的函数关系式;
(3)已知该文具批发部这种笔记本的进价是3元/本,若小明购买此种笔记本超过10本但不超过20本,那么小明购买多少本时,该文具批发部在这次买卖中所获的利润W(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了培养学生的阅读习惯,某校开展了“读好书,助成长”系列活动,并准备购置一批图书,购书前,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,根据统计图所提供的信息,回答下列问题:
(1)本次调查共抽查了名学生,两幅统计图中的m= , n= .
(2)已知该校共有960名学生,请估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校要举办读书知识竞赛,七年(1)班要在班级优胜者2男1女中随机选送2人参赛,求选送的两名参赛同学为1男1女的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1 , 使AA1=BB1=CC1=DD1=![]() a,在边A1B1、B1C1、C1D1、D1A1上分别取点A2、B2、C2、D2 , 使A1A2=B1B2=C1C2=D1D2=
a,在边A1B1、B1C1、C1D1、D1A1上分别取点A2、B2、C2、D2 , 使A1A2=B1B2=C1C2=D1D2=![]() A1B2 , ….依次规律继续下去,则正方形AnBnCnDn的面积为 .
A1B2 , ….依次规律继续下去,则正方形AnBnCnDn的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
(1)请画出△A1B1C1 , 使△A1B1C1与△ABC关于x轴对称;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2 , 并直接写出点B旋转到点B2所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,对角线AC与BD交于点O;在Rt△PMN中,∠MPN=90°.
(1)如图1,若点P与点O重合且PM⊥AD、PN⊥AB,分别交AD、AB于点E、F,请直接写出PE与PF的数量关系;
(2)将图1中的Rt△PMN绕点O顺时针旋转角度α(0°<α<45°).
①如图2,在旋转过程中(1)中的结论依然成立吗?若成立,请证明;若不成立,请说明理由;
②如图2,在旋转过程中,当∠DOM=15°时,连接EF,若正方形的边长为2,请直接写出线段EF的长;
③如图3,旋转后,若Rt△PMN的顶点P在线段OB上移动(不与点O、B重合),当BD=3BP时,猜想此时PE与PF的数量关系,并给出证明;当BD=mBP时,请直接写出PE与PF的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣a|+|2x﹣1|,a∈R. (I)当a=3时,求关于x的不等式f(x)≤6的解集;
(II)当x∈R时,f(x)≥a2﹣a﹣13,求实数a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c过点B(3,0),C(0,3),D为抛物线的顶点.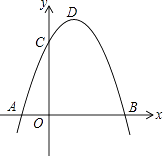
(1)求抛物线的解析式以及顶点坐标;
(2)点C关于抛物线y=﹣x2+bx+c对称轴的对称点为E点,联结BC,BE,求∠CBE的正切值;
(3)点M是抛物线对称轴上一点,且△DMB和△BCE相似,求点M坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com