
【题目】已知:如图,第一象限内的点A,B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且cot∠ACB= ![]()

求:
(1)反比例函数的解析式;
(2)点C的坐标;
(3)∠ABC的余弦值.
【答案】
(1)解:设反比例函数解析式为y= ![]() ,
,
将点A(2,4)代入,得:k=8,
∴反比例函数的解析式y= ![]()
(2)解:过点A作AE⊥x轴于点E,AE与BC交于点F,则CF=2,
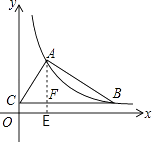
∵cot∠ACB= ![]() =
= ![]() ,
,
∴AF=3,
∴EF=1,
∴点C的坐标为(0,1)
(3)解:当y=1时,由1= ![]() 可得x=8,
可得x=8,
∴点B的坐标为(1,8),
∴BF=BC﹣CF=6,
∴AB= ![]() =3
=3 ![]() ,
,
∴cos∠ABC= ![]() =
= ![]() =
= ![]()
【解析】(1)待定系数法求解可得;(2)作AE⊥x轴于点E,AE与BC交于点F,则CF=2,根据cot∠ACB= ![]() =
= ![]() 得AF=3,即可知EF,从而得出答案;(3)先求出点B的坐标.继而由勾股定理得出AB的长,最后由三角函数可得答案.
得AF=3,即可知EF,从而得出答案;(3)先求出点B的坐标.继而由勾股定理得出AB的长,最后由三角函数可得答案.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣a|+|2x﹣1|,a∈R. (I)当a=3时,求关于x的不等式f(x)≤6的解集;
(II)当x∈R时,f(x)≥a2﹣a﹣13,求实数a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c过点B(3,0),C(0,3),D为抛物线的顶点.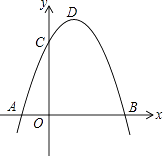
(1)求抛物线的解析式以及顶点坐标;
(2)点C关于抛物线y=﹣x2+bx+c对称轴的对称点为E点,联结BC,BE,求∠CBE的正切值;
(3)点M是抛物线对称轴上一点,且△DMB和△BCE相似,求点M坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知向量 ![]() ,
, ![]() ,
, ![]() .
. 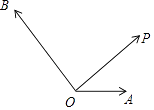
(1)求做:向量 ![]() 分别在
分别在 ![]() ,
, ![]() 方向上的分向量
方向上的分向量 ![]() ,
, ![]() :(不要求写作法,但要在图中明确标出向量
:(不要求写作法,但要在图中明确标出向量 ![]() 和
和 ![]() ).
).
(2)如果点A是线段OD的中点,联结AE、交线段OP于点Q,设 ![]() =
= ![]() ,
, ![]() =
= ![]() ,那么试用
,那么试用 ![]() ,
, ![]() 表示向量
表示向量 ![]() ,
, ![]() (请直接写出结论)
(请直接写出结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=1.5米,BE=2.3米,求拉线CE的长,(精确到0.1米)参考数据 ![]() ≈1.41,
≈1.41, ![]() ≈1.73.
≈1.73. 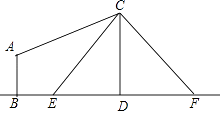
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于非零向量 ![]() 、
、 ![]() 、
、 ![]() 下列条件中,不能判定
下列条件中,不能判定 ![]() 与
与 ![]() 是平行向量的是( )
是平行向量的是( )
A.![]() ∥
∥ ![]() ,
, ![]() ∥
∥ ![]()
B.![]() +3
+3 ![]() =
= ![]() ,
, ![]() =3
=3 ![]()
C.![]() =﹣3
=﹣3 ![]()
D.| ![]() |=3|
|=3| ![]() |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,Rt△ABC中,∠ACB=90°,BC=8,cot∠BAC= ![]() ,点D在边BC上(不与点B、C重合),点E在边BC的延长线上,∠DAE=∠BAC,点F在线段AE上,∠ACF=∠B.设BD=x.
,点D在边BC上(不与点B、C重合),点E在边BC的延长线上,∠DAE=∠BAC,点F在线段AE上,∠ACF=∠B.设BD=x.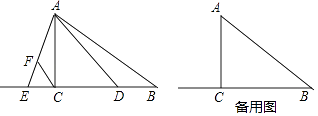
(1)若点F恰好是AE的中点,求线段BD的长;
(2)若y= ![]() ,求y关于x的函数关系式,并写出它的定义域;
,求y关于x的函数关系式,并写出它的定义域;
(3)当△ADE是以AD为腰的等腰三角形时,求线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现与探究:如图,△ABC和△DCE中,AC=BC,DC=EC,∠ACB=∠DCE=45°,点B,C,E三点共线,且BC:CE=2:1,连接AE,BD. 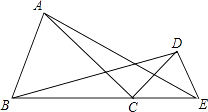
(1)在不添加辅助线和字母的情况下,请在图中找出一对全等三角形(用“≌”表示),并加以证明;
(2)求tan∠BDC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com