
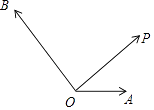
【题目】如图,已知向量 ![]() ,
, ![]() ,
, ![]() .
. 
(1)求做:向量 ![]() 分别在
分别在 ![]() ,
, ![]() 方向上的分向量
方向上的分向量 ![]() ,
, ![]() :(不要求写作法,但要在图中明确标出向量
:(不要求写作法,但要在图中明确标出向量 ![]() 和
和 ![]() ).
).
(2)如果点A是线段OD的中点,联结AE、交线段OP于点Q,设 ![]() =
= ![]() ,
, ![]() =
= ![]() ,那么试用
,那么试用 ![]() ,
, ![]() 表示向量
表示向量 ![]() ,
, ![]() (请直接写出结论)
(请直接写出结论)
【答案】
(1)解:如图,分别过P作OA、OB的平行线,交OA于D,交OB于E,
则向量 ![]() 分别在
分别在 ![]() ,
, ![]() 方向上的分向量是
方向上的分向量是 ![]() ,
, ![]() ;
;
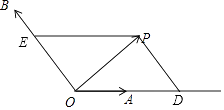
(2)解:如图,∵四边形ODPE是平行四边形,
∴PE∥DO,PE=DO,
∴△OAQ∽△PEQ,
∴ ![]() =
= ![]() =
= ![]() ,
,
∵点A是线段OD的中点,
∴OA= ![]() OD=
OD= ![]() PE,
PE,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =2
=2 ![]() =﹣2
=﹣2 ![]() ,
, ![]() =
= ![]()
![]() =
= ![]()
![]() .
.
∵ ![]() =
= ![]() ﹣
﹣ ![]() =
= ![]() ﹣2
﹣2 ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ﹣2
﹣2 ![]() ,
,
∴ ![]() =
= ![]() ﹣
﹣ ![]() =
= ![]() ﹣2
﹣2 ![]() ﹣
﹣ ![]()
![]() =
= ![]()
![]() ﹣2
﹣2 ![]() .
.
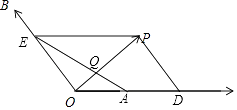
【解析】(1)根据向量加法的平行四边形法则,分别过P作OA、OB的平行线,交OA于D,交OB于E;(2)易得△OAQ∽△PEQ,根据相似三角形对应边成比例得出 ![]() =
= ![]() =
= ![]() =
= ![]() ,那么
,那么 ![]() =2
=2 ![]() =﹣2
=﹣2 ![]() ,
, ![]() =
= ![]()
![]() =
= ![]()
![]() .再求出
.再求出 ![]() =
= ![]() =
= ![]() ﹣2
﹣2 ![]() ,然后根据
,然后根据 ![]() =
= ![]() ﹣
﹣ ![]() 即可求解.
即可求解.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠AOB=90°,AB∥x轴,OB=2,双曲线y=![]() 经过点B,将△AOB绕点B逆时针旋转,使点O的对应点D落在x轴的正半轴上.若AB的对应线段CB恰好经过点O.
经过点B,将△AOB绕点B逆时针旋转,使点O的对应点D落在x轴的正半轴上.若AB的对应线段CB恰好经过点O.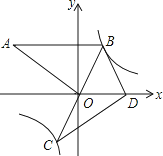
(1)求点B的坐标和双曲线的解析式;
(2)判断点C是否在双曲线上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条抛物线y=﹣x(x﹣2)(0≤x≤2)的一部分,记为C1 , 它与x轴交于O,A1两点,将C1绕点A1旋转180°得到C2 , 交x轴于点A2 , ;将C2绕点A2旋转180°得到C3 , 交x轴于A3;…如此进行下去,直至得到C6 , 若点P(2017,y)在抛物线Cn上,则y= . 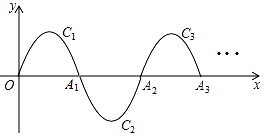
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,将△ABC绕点A顺时针旋转,使点C落在边AB上的点E处,点B落在点D处,连接BD,如果∠DAC=∠DBA,那么 ![]() 的值是 .
的值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE∥BC,且过△ABC的重心,分别与AB,AC交于点D,E,点P是线段DE上一点,CP的延长线交AB于点Q,如果 ![]() =
= ![]() ,那么S△DPQ:S△CPE的值是 .
,那么S△DPQ:S△CPE的值是 . 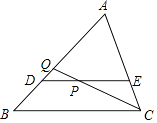
查看答案和解析>>
科目:初中数学 来源: 题型:
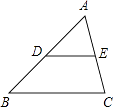
【题目】如图,在△ABC中,点D,E分别是边AB,AC的中点,设 ![]() =
= ![]() ,
, ![]() =
= ![]() .
. 
(1)求向量 ![]() (用向量
(用向量 ![]() ,
, ![]() 的式子表示).
的式子表示).
(2)在图中作出向量 ![]() 在向量
在向量 ![]() ,
, ![]() 方向上的分向量(不要求写作法,但要指出所作图中表示结论的向量).
方向上的分向量(不要求写作法,但要指出所作图中表示结论的向量).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,第一象限内的点A,B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且cot∠ACB= ![]()

求:
(1)反比例函数的解析式;
(2)点C的坐标;
(3)∠ABC的余弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C. 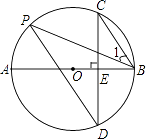
(1)求证:CB∥PD;
(2)若BC=6,sin∠P= ![]() ,求AB的值.
,求AB的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com