
【题目】发现与探究:如图,△ABC和△DCE中,AC=BC,DC=EC,∠ACB=∠DCE=45°,点B,C,E三点共线,且BC:CE=2:1,连接AE,BD. 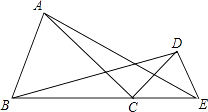
(1)在不添加辅助线和字母的情况下,请在图中找出一对全等三角形(用“≌”表示),并加以证明;
(2)求tan∠BDC的值.
【答案】
(1)解:△BCD≌△ACE,
∵∠ACB=∠DCE,
∴∠ACB+∠ACD=∠DCE+∠ACD,即∠BCD=∠ACE,
在△BCD与△ACE中 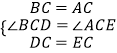 ,
,
∴△BCD≌△ACE(SAS)
(2)解:作AF⊥BE,如图:
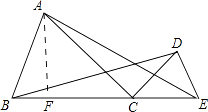
∵BC:CE=2:1,
∴设BC=2k,CE=k,
在Rt△AFC中,AC=BC=2k,∠ACF=45°,
∴FC=ACcos45°=2k× ![]() ,EF=FC+CE=
,EF=FC+CE= ![]() k+k=(
k+k=( ![]() +1)k,
+1)k,
∵∠FAC=45°,
∴AF= ![]() k,
k,
由(1)得△BCD≌△ACE,
∴∠BDC=∠AEC,
∴在Rt△AFE中,tan∠BDC=tan∠AEC= ![]()
【解析】(1)根据SAS证明△BCD与△ACE全等即可;(2)作AF⊥BE,利用三角函数进行解答即可.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,一条抛物线y=﹣x(x﹣2)(0≤x≤2)的一部分,记为C1 , 它与x轴交于O,A1两点,将C1绕点A1旋转180°得到C2 , 交x轴于点A2 , ;将C2绕点A2旋转180°得到C3 , 交x轴于A3;…如此进行下去,直至得到C6 , 若点P(2017,y)在抛物线Cn上,则y= . 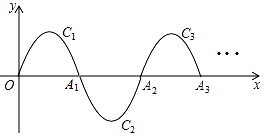
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,第一象限内的点A,B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且cot∠ACB= ![]()

求:
(1)反比例函数的解析式;
(2)点C的坐标;
(3)∠ABC的余弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C. 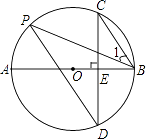
(1)求证:CB∥PD;
(2)若BC=6,sin∠P= ![]() ,求AB的值.
,求AB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,⊙A切y轴于点B,且点A在反比例函数y= ![]() (x>0)的图象上,连接OA交⊙A于点C,且点C为OA中点,则图中阴影部分的面积为( )
(x>0)的图象上,连接OA交⊙A于点C,且点C为OA中点,则图中阴影部分的面积为( ) 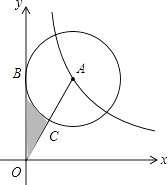
A.4 ![]() ﹣
﹣ ![]()
B.4 ![]()
C.2 ![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A在O的正北方向,B在O的正东方向,且OA=OB.某一时刻,甲车从A出发,以60km/h的速度朝正东方向行驶,与此同时,乙车从B出发,以40km/h的速度朝正北方向行驶.1小时后,位于点O处的观察员发现甲、乙两车之间的夹角为45°,即∠COD=45°,此时,甲、乙两人相距的距离为( ) 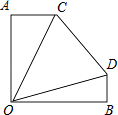
A.90km
B.50 ![]() km
km
C.20 ![]() km
km
D.100km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF. 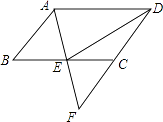
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°. 
(1)求证:AC是⊙O的切线;
(2)求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com