
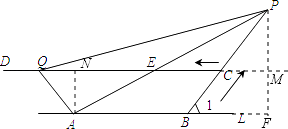
【题目】如图,A,B是直线l上的两点,AB=4厘米,过l外一点C作CD∥l,射线BC与l所组成的锐角为60°,线段BC=2厘米,动点P、Q分别从B、C同时出发,P以1厘米/秒的速度,沿由B向C的方向运动;Q以2厘米/秒的速度,沿由C向D的方向运动,设P、Q运动的时间为t秒,当t>2时,PA交CD于点E. 
(1)用含t的代数式分别表示CE和QE的长;
(2)求△APQ的面积s与t的函数表达式;
(3)当QE恰好平分△APQ的面积时,QE的长是多少?
【答案】
(1)解:由题意知:BP=t,CQ=2t,PC=t﹣2.
∵EC∥AB,
∴ ![]() =
= ![]() ,
,
∴EC= ![]() =
= ![]() ,
,
∴QE=QC﹣EC=2t﹣ ![]() =
= ![]() ;
;
(2)解:如图,作PF⊥L于F,交DC延长线于M,AN⊥CD于N.
在△PBF中,PF=PBsin60°= ![]() t,
t,
∴S△APQ=S△AQE+S△PQE
= ![]() QEAN+
QEAN+ ![]() QEPM=
QEPM= ![]() QEPF
QEPF
= ![]() ×
× ![]() ×
× ![]() t=
t= ![]() (t2﹣2t+4);
(t2﹣2t+4);
(3)解:此时,E为PA的中点,所以C也是PB的中点,
则t﹣2=2,
∴t=4,
∴QE= ![]() =
= ![]() =6(厘米).
=6(厘米).
【解析】(1)根据题意得出BP=t,CQ=2t,PC=t﹣2,再根据EC∥AB,得出 ![]() =
= ![]() ,最后得出EC的值,即可表示出CE和QE的长;(2)以QE为底边,过P引l的垂线作高,根据P的速度可以用t表示出BP,也就能用BP和∠1的正弦函数求出高,那么关键是求QE的长,我们可以根据Q的速度用时间t表示出CQ,那么只要求出CE即可.用相似三角形的对应线段成比例来求CE的长,根据三角形PEC和三角形PAB相似,可得出关于CE、AB、PC、BC的比例式,由BP、BC、AB的值,可以用含t的式子表示出CE,也就表示出了QE,那么可根据三角形的面积公式,得出关于S与t的函数关系式;(3)如果QE恰好平分三角形APQ的面积,那么此时P到CD和CD到l之间的距离就相等,那么C就是PB的中点,可根据BP=2BC求出t的值,然后根据(1)中得出的表示QE的式子,将t代入即可得出QE的值即可.
,最后得出EC的值,即可表示出CE和QE的长;(2)以QE为底边,过P引l的垂线作高,根据P的速度可以用t表示出BP,也就能用BP和∠1的正弦函数求出高,那么关键是求QE的长,我们可以根据Q的速度用时间t表示出CQ,那么只要求出CE即可.用相似三角形的对应线段成比例来求CE的长,根据三角形PEC和三角形PAB相似,可得出关于CE、AB、PC、BC的比例式,由BP、BC、AB的值,可以用含t的式子表示出CE,也就表示出了QE,那么可根据三角形的面积公式,得出关于S与t的函数关系式;(3)如果QE恰好平分三角形APQ的面积,那么此时P到CD和CD到l之间的距离就相等,那么C就是PB的中点,可根据BP=2BC求出t的值,然后根据(1)中得出的表示QE的式子,将t代入即可得出QE的值即可.
【考点精析】通过灵活运用相似三角形的判定与性质和解直角三角形,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)即可以解答此题.


科目:初中数学 来源: 题型:
【题目】已知:如图①,在平面直角坐标系xOy中,A(0,5),C( ![]() ,0),AOCD为矩形,AE垂直于对角线OD于E,点F是点E关于y轴的对称点,连AF、OF.
,0),AOCD为矩形,AE垂直于对角线OD于E,点F是点E关于y轴的对称点,连AF、OF.
(1)求AF和OF的长;
(2)如图②,将△OAF绕点O顺时针旋转一个角α(0°<α<180°),记旋转中的△OAF为△OA′F′,在旋转过程中,设A′F′所在的直线与线段AD交于点P,与线段OD交于点Q,是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时点P坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD的边长为4cm,点E从点A出发沿AD方向以1cm/秒的速度运动,与此同时,点F也从点D出发沿DC方向相同的速度运动,记运动的时间为t(0≤t≤4),AF与BE交于P点. 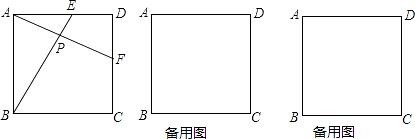
(1)如图,在运动过程中,AF与BE相等吗?请说明理由.
(2)在运动过程中,要使得△BPC是等腰三角形,t应为何值?请画出图形,并求出所有满足条件的t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一副扑克牌中取出的两组牌,分别是红桃1,2,3和方块1,2,3,将它们的背面朝上分别重新洗牌后,再从两组牌中各摸出一张. 
(1)用列表或树状图的方法表示此游戏所有可能出现的结果;
(2)求摸出的两张牌的牌面数字之和不小于4的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+x+c的图像与x轴的一个交点为(2,0),则它与x轴的另一个交点坐标是( )
A.(1,0)
B.(﹣1,0)
C.(2,0)
D.(﹣3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的盒子中有2枚黑棋,x枚白棋,这些棋子除颜色外无其他差别,现从盒中随机摸出一枚棋子(不放回),再随机摸出一枚棋子.
(1)若“摸出两枚棋子的颜色都是白色”是不可能事件,请写出符合条件的一个x值;
(2)当x=2时,“摸出两枚棋子的颜色相同”与“摸出两枚棋子的颜色不同”的概率相等吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业为了解员工给灾区“爱心捐款”的情况,随机抽取部分员工的捐款金额整理绘制成如图所示的直方图,根据图中信息,下列结论错误的是( )
A.样本中位数是200元
B.样本容量是20
C.该企业员工捐款金额的平均数是180元
D.该企业员工最大捐款金额是500元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com