
【题目】已知函数f(x)=|x﹣a|+| ![]() x+1|的最小值为2. (Ⅰ)求实数a的值;
x+1|的最小值为2. (Ⅰ)求实数a的值;
(Ⅱ)若a>0,求不等式f(x)≤4的解集.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图①,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C,D不重合).
(1)如图①,当α=90°时,DE,DF,AD之间满足的数量关系是_____;
(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为DE+DF=![]() AD,请给出证明;
AD,请给出证明;
(3)在(2)的条件下,若旋转过程中∠QPN的边PQ与射线AD交于点E,其他条件不变,探究在整个运动变化过程中,DE,DF,AD之间满足的数量关系,直接写出结论,不用加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+![]() x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
(1)请直接写出二次函数y=ax2+![]() x+c的表达式;
x+c的表达式;
(2)判断△ABC的形状,并说明理由;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请直接写出此时点N的坐标;
(4)若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】过双曲线x2﹣ ![]() =1的右支上一点P,分别向圆C1:(x+4)2+y2=4和圆C2:(x﹣4)2+y2=1作切线,切点分别为M,N,则|PM|2﹣|PN|2的最小值为( )
=1的右支上一点P,分别向圆C1:(x+4)2+y2=4和圆C2:(x﹣4)2+y2=1作切线,切点分别为M,N,则|PM|2﹣|PN|2的最小值为( )
A.10
B.13
C.16
D.19
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂的污水处理程序如下:原始污水必先经过A系统处理,处理后的污水(A级水)达到环保标准(简称达标)的概率为p(0<p<1).经化验检测,若确认达标便可直接排放;若不达标则必须进行B系统处理后直接排放. 某厂现有4个标准水量的A级水池,分别取样、检测.多个污水样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验.混合样本中只要有样本不达标,则混合样本的化验结果必不达标.若混合样本不达标,则该组中各个样本必须再逐个化验;若混合样本达标,则原水池的污水直接排放.
现有以下四种方案,
方案一:逐个化验;
方案二:平均分成两组化验;
方案三:三个样本混在一起化验,剩下的一个单独化验;
方案四:混在一起化验.
化验次数的期望值越小,则方案的越“优”.
(Ⅰ) 若 ![]() ,求2个A级水样本混合化验结果不达标的概率;
,求2个A级水样本混合化验结果不达标的概率;
(Ⅱ) 若 ![]() ,现有4个A级水样本需要化验,请问:方案一,二,四中哪个最“优”?
,现有4个A级水样本需要化验,请问:方案一,二,四中哪个最“优”?
(Ⅲ) 若“方案三”比“方案四”更“优”,求p的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的方程为 ![]() .以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρ2﹣8ρsinθ+15=0. (Ⅰ)写出C1的参数方程和C2的直角坐标方程;
.以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρ2﹣8ρsinθ+15=0. (Ⅰ)写出C1的参数方程和C2的直角坐标方程;
(Ⅱ)设点P在C1上,点Q在C2上,求|PQ|的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是矩形,cot∠ADB= ![]() ,AB=16.点E在射线BC上,点F在线段BD上,且∠DEF=∠ADB.
,AB=16.点E在射线BC上,点F在线段BD上,且∠DEF=∠ADB.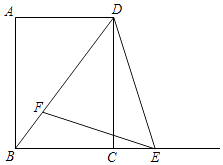
(1)求线段BD的长;
(2)设BE=x,△DEF的面积为y,求y关于x的函数关系式,并写出函数定义域;
(3)当△DEF为等腰三角形时,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,M为CD中点,分别以B、M为圆心,以BC长、MC长为半径画弧,两弧相交于点P,若∠PBC=70°,则∠MPC的度数为( ) 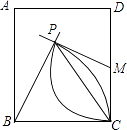
A.55°
B.40°
C.35°
D.20°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com