
分析 (1)根据a、b、c为正实数,且a+b+c=1,可以得到a、b、c的取值范围,因为正的真分数的平方小于它本身,本题得以解决;
(2)首先判断$\sqrt{3a+1}+\sqrt{3b+1}+\sqrt{3c+1}$与4的大小关系,然后对所求的式子进行变形,即可证得结论成立.
解答 解:(1)∵a、b、c为正实数,且a+b+c=1,
∴0<a<1,0<b<1,0<c<1,
∴a2<a,
故答案为:<;
(2)$\sqrt{3a+1}+\sqrt{3b+1}+\sqrt{3c+1}$>4,
理由:方法一:∵$(\sqrt{3a+1}+\sqrt{3b+1})^{2}$
=3a+1+3b+1+2$\sqrt{(3a+1)(3b+1)}$
=3(a+b)+2$\sqrt{9ab+3(a+b)+1}$+2
>[3(a+b)+1]+2$\sqrt{3(a+b)+1}+1$
=$(\sqrt{3(a+b)+1}+1)^{2}$
∴$\sqrt{3a+1}+\sqrt{3b+1}>\sqrt{3(a+b)+1}+1$,
同理可证,$\sqrt{3(a+b)+1}+\sqrt{3c+1}$>$\sqrt{3(a+b+c)+1}+1$,
∴$\sqrt{3a+1}+\sqrt{3b+1}+\sqrt{3c+1}$>$\sqrt{3(a+b)+1}+1+\sqrt{3c+1}$>$\sqrt{3(a+b+c)+1}+1+1$,
∵a+b+c=1,
∴$\sqrt{3(a+b+c)+1}+1+1$=$\sqrt{3+1}+1+1=\sqrt{4}+1+1=2+1+1=4$,
即$\sqrt{3a+1}+\sqrt{3b+1}+\sqrt{3c+1}$>4.
方法二:由(1)知a2<a,则b2<b,c2<c,
∴$\sqrt{3a+1}+\sqrt{3b+1}+\sqrt{3c+1}$=$\sqrt{a+2a+1}+\sqrt{b+2b+1}+\sqrt{c+2c+1}$>$\sqrt{{a}^{2}+2a+1}+\sqrt{{b}^{2}+2b+1}+\sqrt{{c}^{2}+2c+1}$=a+1+b+1+c+1=a+b+c+3,
∵a+b+c=1,
∴a+b+c+3=4,
即$\sqrt{3a+1}+\sqrt{3b+1}+\sqrt{3c+1}$>4.
点评 本题考查二次根式的应用,解题的关键是明确题意,找出所求问题需要的条件,需要注意的是其中不等号的应用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 正方形ABCD,点E在AD上,点F为CE的中点,过点F作CE的垂线交AB,CD于点H,G.
正方形ABCD,点E在AD上,点F为CE的中点,过点F作CE的垂线交AB,CD于点H,G.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
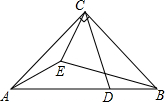 如图,在△ABC中,∠ACB=90°,AC=BC,点D在AB上,AD=9,BD=3,EA=EC,∠ECD=45°,则BE的长为$\frac{3\sqrt{26}}{2}$.
如图,在△ABC中,∠ACB=90°,AC=BC,点D在AB上,AD=9,BD=3,EA=EC,∠ECD=45°,则BE的长为$\frac{3\sqrt{26}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解电影《寻龙诀》在我市中学生中的口碑适合全面普查方式收集数据 | |
| B. | 若甲队成绩的方差是2,乙队成绩的方差是3,说明甲队成绩比乙队成绩稳定 | |
| C. | 一组数据4,6,7,6,7,8,9,中位数和众数都是6 | |
| D. | 明天下雨的概率为1%,所以明天一定不下雨 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com