
【题目】如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,﹣3)
(1)求此二次函数的解析式及顶点坐标.
(2)设点P是该抛物线上的动点,当△ABP的面积等于△ABC面积的![]() 时,求出点P的坐标.
时,求出点P的坐标.
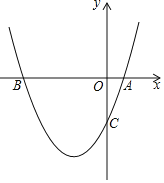
【答案】(1)y=x2+2x﹣3,顶点坐标(﹣1,﹣4);(2)P点坐标为(﹣4,5),(2,5).
【解析】
(1)将点A、C的坐标分别代入函数解析式,列出关于b、c的方程组,通过解方程组求得它们的值即可;
(2)根据抛物线与坐标轴交点的求法求得点B的坐标,结合三角形的面积公式求得△ABC的面积=6,进而求得△ABP的面积=10,根据△ABP的面积可以计算出点P的纵坐标的值,然后再利用二次函数解析式计算出点P的横坐标即可.
解:(1)根据题意得:![]() .
.
解得:b=2,c=﹣3,
∴二次函数的解析式为y=x2+2x﹣3,
∵y=x2+2x﹣3=(x+1)2﹣4;
∴顶点坐标(﹣1,﹣4);
(2)当y=0时,x2+2x﹣3=0,解得x1=﹣3,x2=1,则B(﹣3,0),A(1,0),
∴AB=4
∵C(0,﹣3)
∴△ABC的面积=![]() ×4×3=6,
×4×3=6,
∵△ABP的面积等于△ABC面积的![]()
∴△ABP的面积=![]() ×6=10,
×6=10,
∴![]() 4×|yp|=10
4×|yp|=10
∴|yp|=5,
∴yp=±5,
当yp=5时 解方程x2+2x﹣3=5得x1=﹣4,x2=2,此时P点坐标为(﹣4,5),(2,5);
当yp=﹣5时,方程x2+2x﹣3=﹣5没有实数解,
∴P点坐标为(﹣4,5),(2,5).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某商店准备销售一种多功能旅行背包,计划从厂家以每个30元的价格进货,经过市场发现当每个背包的售价为40元时,月均销量为280个,售价每增长2元,月均销量就相应减少20个.
(1)若使这种背包的月均销量不低于130个,每个背包售价应不高于多少元?
(2)在(1)的条件下,当该这种书包销售单价为多少元时,销售利润是3120元?
(3)这种书包的销售利润有可能达到3700元吗?若能,请求出此时的销售单价;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线y=ax2+bx+c的图象经过(﹣1,0),对称轴x=1,则下列三个结论:①abc<0;②10a+3b+c>0;③am2+bm+a≥0.正确的结论为_____(填序号).
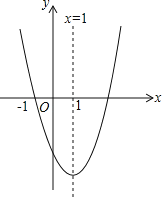
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某市连续5天的天气情况.

(1)利用方差判断该市这5天的日最高气温波动大还是日最低气温波动大;
(2)根据如图提供的信息,请再写出两个不同类型的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,BC∥AD,∠B=90°,AD边落在平面直角坐标系的x轴上,且点A(5,0)、C(0,3)、AD=2.点P从点E(﹣5,0)出发,沿x轴向点A以每秒1个单位长度的速度运动,到达点A时停止运动.运动时间为t秒.
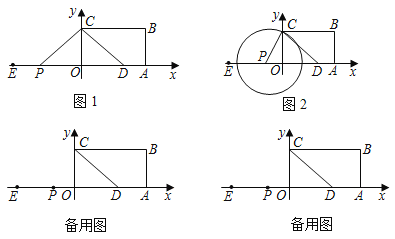
(1)∠BCD的度数为______°.
(2)当t=_____时,△PCD为等腰三角形.
(3)如图2,以点P为圆心,PC为半径作⊙P.
①求当t为何值时,⊙P与四边形ABCD的一边(或边所在的直线)相切.
②当t______时,⊙P与四边形ABCD的交点有两个;当t_____时,⊙P与四边形ABCD的交点有三个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么,当t为何值时,△POQ与△AOB相似?
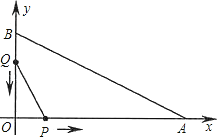
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 内接于
内接于![]() ,
,![]() 平分
平分![]() .
.
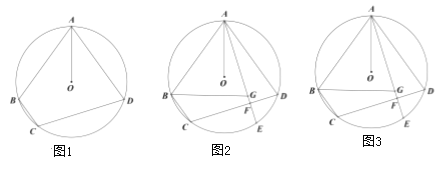
(1)如图1,求证:![]() ;
;
(2)如图2,![]() ,弦
,弦![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,点![]() 是
是![]() 上一点,连接
上一点,连接![]() ,
,![]() ,若
,若![]() ,
,![]() ,求线段
,求线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:
已知二次函数y=﹣![]() x2+
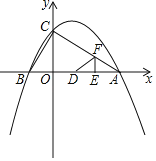
x2+![]() x+2的图象与x轴交于A,B两点(点B在点A的左侧),与y轴交于点C.
x+2的图象与x轴交于A,B两点(点B在点A的左侧),与y轴交于点C.
(1)求点A,B,C的坐标;
(2)求证:△ABC为直角三角形;
(3)如图,动点E,F同时从点A出发,其中点E以每秒2个单位长度的速度沿AB边向终点B运动,点F以每秒![]() 个单位长度的速度沿射线AC方向运动.当点F停止运动时,点E随之停止运动.设运动时间为t秒,连结EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.当点F在AC上时,是否存在某一时刻t,使得△DCO≌△BCO?(点D不与点B重合)若存在,求出t的值;若不存在,请说明理由.
个单位长度的速度沿射线AC方向运动.当点F停止运动时,点E随之停止运动.设运动时间为t秒,连结EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.当点F在AC上时,是否存在某一时刻t,使得△DCO≌△BCO?(点D不与点B重合)若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com