
【题目】若所求的二次函数图象与抛物线y=2x2-4x-1有相同的顶点,并且在对称轴的左侧,y随x的增大而增大,在对称轴的右侧,y随x的增大而减小,则所求二次函数的表达式为( )
A. y=-x2+2x+4 B. y=-ax2-2ax-3(a>0)
C. y=-2x2-4x-5 D. y=ax2-2ax+a-3(a<0)
【答案】D
【解析】
先由顶点公式(-![]() ,
,![]() )求出抛物线y=2x2-4x-1的顶点坐标为(1,-3),根据题意得所求的二次函数的解析式的顶点坐标是(1,-3),且抛物线开口向下.再分别确定选项中的顶点坐标和开口方向即可求解.
)求出抛物线y=2x2-4x-1的顶点坐标为(1,-3),根据题意得所求的二次函数的解析式的顶点坐标是(1,-3),且抛物线开口向下.再分别确定选项中的顶点坐标和开口方向即可求解.
解:抛物线y=2x2-4x-1的顶点坐标为(1,-3),根据题意得所求的二次函数的解析式的顶点坐标是(1,-3),且抛物线开口向下.
A、抛物线开口向下,顶点坐标是(1,5),故选项错误;
B、抛物线开口向下,顶点坐标是(1,-3a-3),故选项错误;
C、抛物线开口向下,顶点坐标是(-1,-3),故选项错误;
D、抛物线开口向下,顶点坐标是(1,-3),故选项正确.
故选:D.


科目:初中数学 来源: 题型:
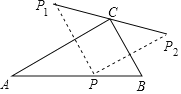
【题目】如图,△ABC中,∠ACB=90°,∠A=30°,AC=6,点P在边AB上运动(不与端点重合),点P关于直线AC,BC对称的点分别为P1,P2.则在点P的运动过程中,线段P1P2的长度m的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某庄有甲、乙两家草莓采摘园的草莓销售价格相同,春节期间,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为![]() (千克),在甲园所需总费用为
(千克),在甲园所需总费用为![]() (元),在乙园所需总费用为
(元),在乙园所需总费用为![]() (元),
(元),![]() 、
、![]() 与
与![]() 之间的函数关系如图所示.
之间的函数关系如图所示.

(1)甲采摘园的门票是_____元,两个采摘园优惠前的草莓单价是每千克____元;
(2)当![]() 时,求
时,求![]() 与
与![]() 的函数表达式;
的函数表达式;
(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,请回答下列问题
材料一:我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,即已知三角形的三边长,求它的面积.用现代式子表示即为:S=![]() …①(其中a,b,c为三角形的三边长,S为面积)而另一个文明古国古希腊也有求三角形面积的“海伦公式”;S=
…①(其中a,b,c为三角形的三边长,S为面积)而另一个文明古国古希腊也有求三角形面积的“海伦公式”;S=![]() ……②(其中p=
……②(其中p=![]() )
)
材料二:对于平方差公式:a2﹣b2=(a+b)(a﹣b)
公式逆用可得:(a+b)(a﹣b)=a2﹣b2,
例:a2﹣(b+c)2=(a+b+c)(a﹣b﹣c)
(1)若已知三角形的三边长分别为3、4、5,请试分别运用公式①和公式②,计算该三角形的面积;
(2)你能否由公式①推导出公式②?请试试.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB∥DE,AC∥DF,AC=DF下列条件中,不能判断△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )

A.带①去B.带②去C.带③去D.带①和②去
查看答案和解析>>
科目:初中数学 来源: 题型:
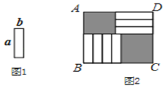
【题目】7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.当BC的长度变化时,按照同样的放置方式,左上角与右下角的阴影部分的面积的差S始终保持不变,则a,b满足的关系是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知△ABC为等边三角形,动点D在边AC上,动点P在边BC上,若这两点分别从C、B点同时出发,以相同的速度由C向A和由B向C运动,连结AP、BD交于Q,两点运动的过程中,AP=BD成立吗?请证明你的结论.
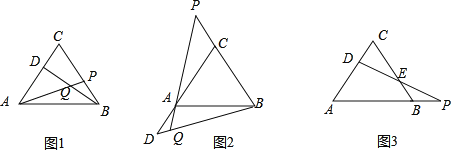
(2)如果把原题中的“动点D在边AC上,动点P在边BC上,”改为:“动点D在射线CA上、动点P在射线BC上运动,”其他条件不变,如图2所示,AP=BD还成立吗?说明理由,并求出∠BQP的大小.
(3)如果把原题中的“动点P在边BC上”,改为“动点P在射线AB上运动”,连结DP交BC于E,其他条件不变,如图3,则动点D、P在运动过程中,请你写出DE与PE的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com