练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知二次函数y=x2+bx+3的图象与x轴正半轴交于B、C两点，BC=2，则b的值为（ ）

    A．4 B．﹣4 C．±4 D．﹣5

    【答案】B

    【解析】

    试题分析：设C（m，0），B（n，0），则n﹣m=2，根据抛物线与x轴的交点问题得到m、n为方程x2+bx+3=0的两根，则利用根与系数的关系得到m+n=﹣b，mn=3，由于（n﹣m）2=4，则（m+n）2﹣4mn=4，即b2﹣4×3=4，然后解关于b的方程即可．

    解：设C（m，0），B（n，0），则m﹣n=2，

    ∵m、n为方程x2+bx+3=0的两根，

    ∴m+n=﹣b＞0，mn=3，

    ∵（n﹣m）2=4，

    ∴（m+n）2﹣4mn=4，

    ∴b2﹣4×3=4，解得b=4（舍去）或b=﹣4，

    即b的值为﹣4．

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，点M，N分别是∠AOB的边OA，OB上的点，OM＝3，ON＝7，在∠AOB内有一点G，到边OA，OB的距离相等，且满足GM＝GN．

    （1）尺规作图：画出点G（要求：保留作图痕迹）；

    （2）试证明：∠OMG+∠ONG＝180°；

    （3）若P，Q分别是射线OA，OB上的动点，且满足GP＝GQ，则当OP＝4时，OQ的长度为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点 A,B,C 的坐标分别是（2,1），（6,1），（3，5），若△A1B1C1 与△ABC 关于x 轴对称

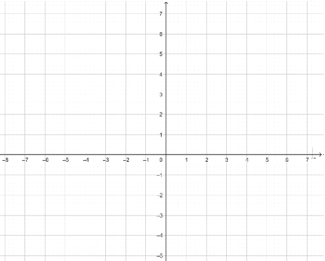
    （1）在平面直角坐标系中画出△A1B1C1，并写出 A1,B1,C1 三个点的坐标

    （2）求出△A1B1C1的面积

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知△ABC中，∠B＝50°，∠C＝70°，AD是△ABC的角平分线，DE⊥AB于E点．

    （1）求∠EDA的度数；

    （2）AB＝10，AC＝8，DE＝3，求S△ABC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若所求的二次函数图象与抛物线y＝2x2－4x－1有相同的顶点，并且在对称轴的左侧，y随x的增大而增大，在对称轴的右侧，y随x的增大而减小，则所求二次函数的表达式为（ ）

    A. y＝－x2＋2x＋4 B. y＝－ax2－2ax－3(a＞0)

    C. y＝－2x2－4x－5 D. y＝ax2－2ax＋a－3(a＜0)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】徐州至北京的高铁里程约为700km，甲、乙两人从徐州出发，分别乘坐“徐州号”高铁A与“复兴号”高铁B前往北京．已知A车的平均速度比B车的平均速度慢80km/h，A车的行驶时间比B车的行驶时间多40%，两车的行驶时间分别为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司销售某一种新型通讯产品，已知每件产品的进价为4万元，每月销售该种产品的总开支(不含进价)总计11万元.在销售过程中发现，月销售量夕(件)与销售单价x (万元)之间存在着如图所示的一次函数关系、

    (1)求y关于x的函数关系式(直接写出结果)

    (2)试写出该公司销售该种产品的月获利z(万元)关于销售单价x(万元)的函数关系式、当销售单价x为何值时，月获利最大?并求这个最大值(月获利一月销售额一月销售产品总进价一月总开支)

    (3)若公司希望该产品一个月的销售获利不低于5万元，借助(2)中函数的图象，请你帮助该公司确定销售单价的范围.在此情况下，要使产品销售量最大，你认为销售单价应定为多少万元

    查看答案和解析>>

    科目：初中数学 来源： 题型：

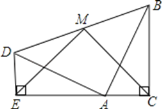
    【题目】两个全等的含30°，60°角的三角板ADE和三角板ABC如图所示放置，E，A，C三点在一条直线上，连接BD，取BD的中点M，连接ME，MC．试判断△EMC的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知四边形ABCD中，∠ABC=90°，∠ADC=90°，AB=6，CD=4，BC的延长线与AD的延长线交于点E．

    （1）若∠A=60°，求BC的长；

    （2）若sinA=，求AD的长．

    （注意：本题中的计算过程和结果均保留根号）

    查看答案和解析>>

    同步练习册答案