
【题目】如图,点M,N分别是∠AOB的边OA,OB上的点,OM=3,ON=7,在∠AOB内有一点G,到边OA,OB的距离相等,且满足GM=GN.
(1)尺规作图:画出点G(要求:保留作图痕迹);
(2)试证明:∠OMG+∠ONG=180°;
(3)若P,Q分别是射线OA,OB上的动点,且满足GP=GQ,则当OP=4时,OQ的长度为 .

【答案】(1)见解析;(2)见解析;(3)4或6
【解析】
(1)作OP平分∠AOB,作线段MN的垂直平分线EF,EF交OP于点G,点G即为所求;
(2)证明△OGK≌△OGH(AAS),推出OK=OH,GK=GH,由GM=GN,∠GKM=∠GHN=90°,推出Rt△GKM≌Rt△GHN(HL),再利用全等三角形的性质,四边形内角和定理解决问题;
(3)首先求出OK=OH=5,PK=1,然后分两种情形分别求解即可解决问题.
解:(1)如图,点G即为所求.
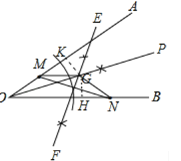
(2)证明:作GK⊥OA于K,GH⊥OB于H.
∵∠GOK=∠GOH,∠GKO=∠GHO=90°,OG=OG,
∴△OGK≌△OGH(AAS),
∴OK=OH,GK=GH,
∵GM=GN,∠GKM=∠GHN=90°,
∴Rt△GKM≌Rt△GHN(HL),
∴∠KGM=∠HGN,
∴∠MGN=∠KGH,
∵∠KGH+∠AOB=180°,
∴∠MGN+∠AOB=180°,
∴∠OMG+∠ONG=180°;
(3)如图,
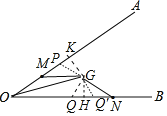
∵OK=OH,MK=NH,
∴OM+ON=OK﹣KM+OH+HN=2OK=10,
∴OK=OH=5,
∵OP=4,
∴PK=5﹣4=1,
∵GP=GQ,
∴当点Q在线段OH上时,OQ=OP=4,
当点Q′在OH的延长线上时,OQ′=5+1=6,
故答案为4或6.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论,①△BDF是等腰三角形;②DE=BD+CE;③若∠A=50°,∠BFC=105°;④BF=CF.其中正确的有( )
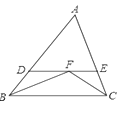
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
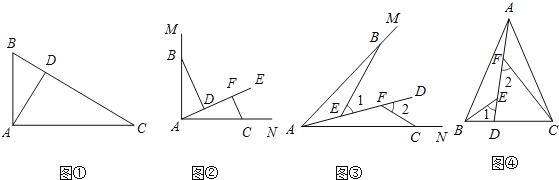
【题目】问题情境:如图①,在直角三角形ABC中,∠BAC=90,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
(1)特例探究:如图②,∠MAN=90,射线AE在这个角的内部,点B.C在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;
(2)归纳证明:如图③,点B,C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)拓展应用:如图④,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E.F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为18,求△ACF与△BDE的面积之和是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课间,小聪拿着老师的等腰直角三角板玩,不小心掉到两墙之间(如图),![]() ,
,![]() ,每块砌墙用的砖块厚度为
,每块砌墙用的砖块厚度为![]() ,小聪很快就知道了两个墙脚之间的距离
,小聪很快就知道了两个墙脚之间的距离![]() 的长为______
的长为______![]()
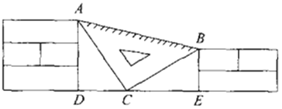
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,∠A=30°,AC=6,点P在边AB上运动(不与端点重合),点P关于直线AC,BC对称的点分别为P1,P2.则在点P的运动过程中,线段P1P2的长度m的取值范围是_____.
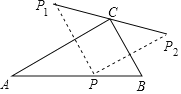
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】何老师将五顶帽子分别给五位同学戴上,每位同学都知道有三顶白色、两顶黑色,但不知道自己所戴帽子的颜色.现将五位同学分别安排在两个小房子中(如图),不许他们摘下帽子看或回头看,也不许互相交流,经过一段时间,其中一位同学可以最快报出白己所戴帽子的颜色,则该同学的编号是( )
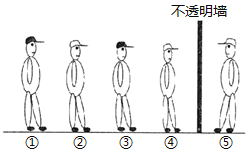
A.①B.②C.③D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠A=38°,D,E分别为AB,AC上一点,将△BCD,△ADE沿CD,DE翻折,点A,B恰好重合于点P处,则∠ACP=_________.
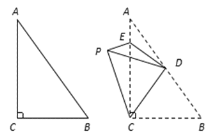
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题
(1)画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1,并写出点C1的坐标;
(2)画出将△ABC关于原点O对称的图形△A2B2C2,并写出点C2的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com