练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，△ABC中，∠ABC与∠ACB的平分线交于点F，过点F作DE∥BC交AB于点D，交AC于点E，那么下列结论，①△BDF是等腰三角形；②DE＝BD+CE；③若∠A＝50°，∠BFC＝105°；④BF＝CF．其中正确的有（　　）

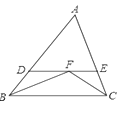
    A.1个B.2个C.3个D.4个

    【答案】B

    【解析】

    根据平行线的性质和角平分线的定义以及等腰三角形的判定和性质解答．

    ∵DE∥BC，
    ∴∠DFB=∠FBC，
    ∵BF平分∠ABC，
    ∴∠DBF=∠FBC，
    ∴∠DBF=∠DFC，
    ∴△BDF是等腰三角形，故①正确；
    ∴BD=DF，
    同理可得：EC=FE，
    ∴DE=BD+CE，故②正确；
    ∵∠A=50°，∴∠BFC=90°+∠A=90°+25°=115°，故③错误；
    无法得出BF=FC，故④错误；
    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知DC∥FP，∠1=∠2，∠FED=28°，∠AGF=80°，FH平分∠EFG.

    （1）证明：DC∥AB；

    （2）求∠PFH的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有甲、乙两个箱子，其中甲箱内有颗球，分别标记号码，且号码为不重复的整数，乙箱内没有球．已知小育从甲箱内拿出颗球放入乙箱后，乙箱内球的号码的中位数为．若此时甲箱内有颗球的号码小于，有颗球的号码大于，若他们的中位数都为，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形中，点在边上，点在边的延长线上，且．

    求证：；

    将按逆时针方向至少旋转多少度才能与重合，旋转中心是什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某数学兴趣小组对关于的方程提出了下列问题．

    若使方程为一元二次方程，是否存在？若存在，求出并解此方程．

    若使方程为一元一次方程，是否存在？若存在，请求出．你能解决这个问题吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】感知：如图1，在中，D、E分别是AB、AC两边的中点，延长DE至点F，使，连结易知≌．

    探究：如图2，AD是的中线，BE交AC于点E，交AD于点F，且，求证：．

    应用：如图3，在中，，，，DE是的中位线过点D、E作，分别交边BC于点F、G，过点A作，分别与FD、GE的延长线交于点M、N，则四边形MFGN周长C的取值范围是______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

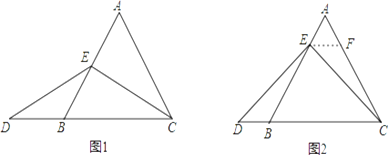
    【题目】已知，在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且ED＝EC．

    （1）（特殊情况，探索结论）

    如图1，当点E为AB的中点时，确定线段AE与DB的大小关系，请你直接写出结论：

    AE　 　DB（填“＞”、“＜”或“＝”）．

    （2）（特例启发，解答题目）

    如图2，当点E为AB边上任意一点时，确定线段AE与DB的大小关系，请你直接写出结论，AE　 　DB（填“＞”、“＜”或“＝”）；理由如下，过点E作EF∥BC，交AC于点F．（请你将解答过程完整写下来）．

    （3）（拓展结论，设计新题）

    在等边三角形ABC中，点E在直线AB上，点D在线段CB的延长线上，且ED＝EC，若△ABC的边长为1，AE＝2，求CD的长.（请你画出相应图形，并直接写出结果）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等边△ABC中，点D，E分别在边BC，AC上，且DE∥AB，过点E作EF⊥DE，交BC的延长线于点F，

    （1）求∠F的度数；

    （2）若CD＝5，求DF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点M，N分别是∠AOB的边OA，OB上的点，OM＝3，ON＝7，在∠AOB内有一点G，到边OA，OB的距离相等，且满足GM＝GN．

    （1）尺规作图：画出点G（要求：保留作图痕迹）；

    （2）试证明：∠OMG+∠ONG＝180°；

    （3）若P，Q分别是射线OA，OB上的动点，且满足GP＝GQ，则当OP＝4时，OQ的长度为　 　．

    查看答案和解析>>

    同步练习册答案