
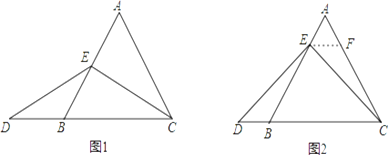
【题目】已知,在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC.
(1)(特殊情况,探索结论)
如图1,当点E为AB的中点时,确定线段AE与DB的大小关系,请你直接写出结论:
AE DB(填“>”、“<”或“=”).
(2)(特例启发,解答题目)
如图2,当点E为AB边上任意一点时,确定线段AE与DB的大小关系,请你直接写出结论,AE DB(填“>”、“<”或“=”);理由如下,过点E作EF∥BC,交AC于点F.(请你将解答过程完整写下来).
(3)(拓展结论,设计新题)
在等边三角形ABC中,点E在直线AB上,点D在线段CB的延长线上,且ED=EC,若△ABC的边长为1,AE=2,求CD的长.(请你画出相应图形,并直接写出结果).
【答案】(1)=;(2)=;理由见解析;(3)3.
【解析】
(1)由E为等边三角形AB边的中点,利用三线合一得到CE垂直于AB,且CE为角平分线,由ED=EC,利用等边对等角及等腰三角形的性质得到一对角相等,利用等角对等边即可得证;
(2)AE=DB,理由如下,过点E作EF∥BC,交AC于点F,由三角形ABC为等边三角形,得到三角形AEF为等边三角形,进而得到AE=EF=AF,BE=FC,再由ED=EC,以及等式的性质得到夹角相等,利用SAS得到三角形BDE与三角形EFC全等,利用全等三角形对应边相等得到DB=EF,等量代换即可得证;
(3)点E在AB延长线上时,如图所示,同理可得△DBE≌△EFC,由BC+DB求出CD的长即可.
(1)当E为AB的中点时,AE=DB;
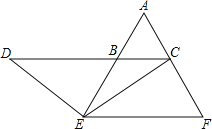
(2)AE=DB,理由如下,过点E作EF∥BC,交AC于点F,
证明:∵△ABC为等边三角形,
∴△AEF为等边三角形,
∴AE=EF,BE=CF,
∵ED=EC,
∴∠D=∠ECD,
∵∠DEB=60°-∠D,∠ECF=60°-∠ECD,
∴∠DEB=∠ECF,
在△DBE和△EFC中,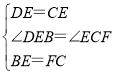 ,
,
∴△DBE≌△EFC(SAS),
∴DB=EF,
则AE=DB;
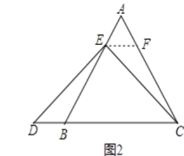
(3)点E在AB延长线上时,如图所示,同理可得△DBE≌△EFC,
∴DB=EF=2,BC=1,
则CD=BC+DB=3.
故答案为:(1)=;(2)=(3)3


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() 过
过![]() ,
,![]() ,
,![]() 三点,点
三点,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,动点
,动点![]() 在抛物线上.
在抛物线上.

![]() ________,
________,![]() ________,点
________,点![]() 的坐标为________;(直接填写结果)
的坐标为________;(直接填写结果)
![]() 是否存在点
是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角边的直角三角形?若存在,求出所有符合条件的点
为直角边的直角三角形?若存在,求出所有符合条件的点![]() 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
![]() 过动点
过动点![]() 作
作![]() 垂直
垂直![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线.垂足为
轴的垂线.垂足为![]() ,连接
,连接![]() ,当线段
,当线段![]() 的长度最短时,求出点
的长度最短时,求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1, △ABC和△CDE均为等腰三角形,AC=BC, CD=CE, AC>CD, ∠ACB=∠DCE=a,且点A、D、E在同一直线上,连结BE.

(1)求证: AD=BE.
(2)如图2,若a=90°,CM⊥AE于E.若CM=7, BE=10, 试求AB的长.
(3)如图3,若a=120°, CM⊥AE于E, BN⊥AE于N, BN=a, CM=b,直接写出AE的值(用a, b 的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论,①△BDF是等腰三角形;②DE=BD+CE;③若∠A=50°,∠BFC=105°;④BF=CF.其中正确的有( )
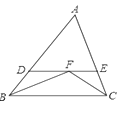
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,在平面直角坐标系中,点M是二次函数![]() 图象上一点,过点M作
图象上一点,过点M作![]() 轴,如果二次函数
轴,如果二次函数![]() 的图象与
的图象与![]() 关于l成轴对称,则称
关于l成轴对称,则称![]() 是
是![]() 关于点M的伴随函数
关于点M的伴随函数![]() 如图2,在平面直角坐标系中,二次函数
如图2,在平面直角坐标系中,二次函数![]() 的函数表达式是
的函数表达式是![]() ,点M是二次函数
,点M是二次函数![]() 图象上一点,且点M的横坐标为m,二次函数
图象上一点,且点M的横坐标为m,二次函数![]() 是
是![]() 关于点M的伴随函数.
关于点M的伴随函数.



![]() 若
若![]() ,
,
![]() 求
求![]() 的函数表达式.
的函数表达式.
![]() 点
点![]() ,
,![]() 在二次函数
在二次函数![]() 的图象上,若
的图象上,若![]() ,a的取值范围为______.
,a的取值范围为______.
![]() 过点M作
过点M作![]() 轴,
轴,
![]() 如果
如果![]() ,线段MN与
,线段MN与![]() 的图象交于点P,且MP:
的图象交于点P,且MP:![]() :3,求m的值.
:3,求m的值.
![]() 如图3,二次函数
如图3,二次函数![]() 的图象在MN上方的部分记为
的图象在MN上方的部分记为![]() ,剩余的部分沿MN翻折得到
,剩余的部分沿MN翻折得到![]() ,由
,由![]() 和
和![]() 所组成的图象记为
所组成的图象记为![]() .以
.以![]() 、
、![]() 为顶点在x轴上方作正方形
为顶点在x轴上方作正方形![]() 直接写出正方形ABCD与G有三个公共点时m的取值范围.
直接写出正方形ABCD与G有三个公共点时m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市出租汽车收费标准为:![]() 以内(含
以内(含![]() )收费
)收费![]() 元;超出
元;超出![]() 的部分,每千米收费
的部分,每千米收费![]() 元.
元.
(1)写出车费![]() 元与行驶路程x(km)之间的函数关系式(
元与行驶路程x(km)之间的函数关系式(![]() ≥4);
≥4);
(2)某人乘出租汽车行驶了5 km,应付多少车费;
(3)若某人付了![]() 元车费,那么出租车行驶了多远.
元车费,那么出租车行驶了多远.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,△ABC中,∠BAC=90°,AB=AC,D,E在BC上,∠DAE=45°,为了探究BD,DE,CE之间的等量关系,现将△AEC绕A顺时针旋转90°后成△AFB,连接DF,经探究,你所得到的BD,DE,CE之间的等量关系式是 ;(无须证明)
(2)如图2,在△ABC中,∠BAC=120°,AB=AC,D,E在BC上,∠DAE=60°,∠ADE=45°,试仿照(1)的方法,利用图形的旋转变换,探究BD,DE,CE之间的等量关系,并证明你的结论.
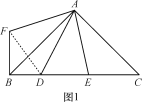
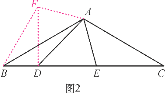
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图①,在直角三角形ABC中,∠BAC=90,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
(1)特例探究:如图②,∠MAN=90,射线AE在这个角的内部,点B.C在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;
(2)归纳证明:如图③,点B,C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)拓展应用:如图④,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E.F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为18,求△ACF与△BDE的面积之和是多少?
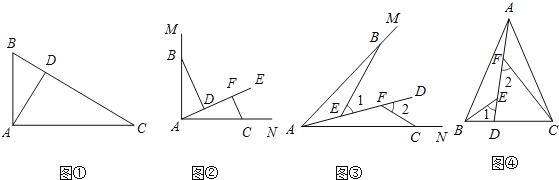
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠A=38°,D,E分别为AB,AC上一点,将△BCD,△ADE沿CD,DE翻折,点A,B恰好重合于点P处,则∠ACP=_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com