
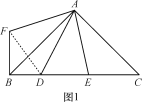
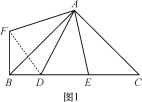
【题目】(1)如图1,△ABC中,∠BAC=90°,AB=AC,D,E在BC上,∠DAE=45°,为了探究BD,DE,CE之间的等量关系,现将△AEC绕A顺时针旋转90°后成△AFB,连接DF,经探究,你所得到的BD,DE,CE之间的等量关系式是 ;(无须证明)
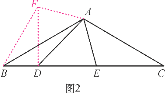
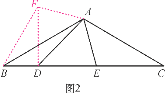
(2)如图2,在△ABC中,∠BAC=120°,AB=AC,D,E在BC上,∠DAE=60°,∠ADE=45°,试仿照(1)的方法,利用图形的旋转变换,探究BD,DE,CE之间的等量关系,并证明你的结论.
【答案】(1) BD2+CE2=DE2; (2) BD2+DE2=CE2,证明见解析.
【解析】
(1)将△AEC绕A顺时针旋转90°后成△AFB,可证△AEC≌△AFB,故BF=CE,旋转角∠FAE=90°,又∠DAE=45°,故∠FAD=∠FAE∠DAE=45°,易证△AFD≌△AED,故FD=DE,因为△ABC中,∠BAC=90°,AB=AC,所以∠ABC=∠FAB=45°,从而可得∠FAD=90°,在Rt△FBD中,由勾股定理得线段BD、DE、CE之间的等量关系式;
(2)方法同(1),由∠ADE=45°可得∠ADF=45°,故∠BDF=90°,斜边BF=CE,直角边DF=DE,由勾股定理建立等量关系.
(1) BD2+CE2=DE2;
(2)CE2=BD2+DE2.
证明:将△AEC绕点A顺时针旋转120 °得到△AFB,连接FD.
由旋转的性质可得△AEC≌△AFB,∴AF=AE,BF=CE,∠FAB=∠EAC.
∴∠FAE=∠FAB+∠BAE=∠EAC+∠BAE=∠BAC=120 °.
又∵∠DAE=60 °,
∴∠FAD=∠EAD=60 °.
在△ADF和△ADE中,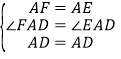
∴△ADF≌△ADE(SAS).
∴FD=DE,∠ADF=∠ADE.
∵∠ADE=45 °,
∴∠ADF=45 °,故∠BDF=90 °.
在Rt△BDF中,由勾股定理,得BF2=BD2+DF2.
∴CE2=BD2+DE2.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】形如:![]() 的函数叫二次函数,它的图象是一条抛物线.类比一元一次方程的解可以看成两条直线的交点的横坐标;则一元二次方程
的函数叫二次函数,它的图象是一条抛物线.类比一元一次方程的解可以看成两条直线的交点的横坐标;则一元二次方程![]() 的解可以看成抛物线
的解可以看成抛物线![]() 与直线
与直线![]() (
(![]() 轴)的交点的横坐标;也可以看成是抛物线
轴)的交点的横坐标;也可以看成是抛物线![]() 与直线
与直线![]() ________的交点的横坐标;也可以看成是抛物线
________的交点的横坐标;也可以看成是抛物线![]() ________与直线
________与直线![]() 的交点的横坐标;
的交点的横坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组对关于![]() 的方程
的方程![]() 提出了下列问题.
提出了下列问题.
![]() 若使方程为一元二次方程,
若使方程为一元二次方程,![]() 是否存在?若存在,求出
是否存在?若存在,求出![]() 并解此方程.
并解此方程.
![]() 若使方程为一元一次方程,
若使方程为一元一次方程,![]() 是否存在?若存在,请求出.你能解决这个问题吗?
是否存在?若存在,请求出.你能解决这个问题吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC.
(1)(特殊情况,探索结论)
如图1,当点E为AB的中点时,确定线段AE与DB的大小关系,请你直接写出结论:
AE DB(填“>”、“<”或“=”).
(2)(特例启发,解答题目)
如图2,当点E为AB边上任意一点时,确定线段AE与DB的大小关系,请你直接写出结论,AE DB(填“>”、“<”或“=”);理由如下,过点E作EF∥BC,交AC于点F.(请你将解答过程完整写下来).
(3)(拓展结论,设计新题)
在等边三角形ABC中,点E在直线AB上,点D在线段CB的延长线上,且ED=EC,若△ABC的边长为1,AE=2,求CD的长.(请你画出相应图形,并直接写出结果).
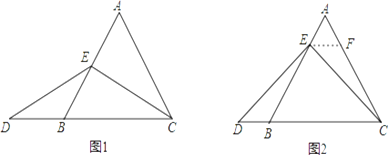
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农夫将苹果树种在正方形的果园内,为了保护苹果树不受风吹,他在苹果树的周围种上针叶树.在下图里,你可以看到农夫所种植苹果树的列数(n)和苹果树数量及针叶树数量的规律:当n为某一个数值时,苹果树数量会等于针叶树数量,则n为___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F,

(1)求∠F的度数;
(2)若CD=5,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,L1反映了某公司产品的销售收入![]() (元)与销售量
(元)与销售量![]() 的函数关系,L2反映了该公司产品的销售成本
的函数关系,L2反映了该公司产品的销售成本![]() (元)与销售量
(元)与销售量![]() 的函数关系,根据图象解答问题:
的函数关系,根据图象解答问题:
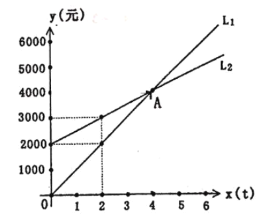
(1)分别求出销售收入![]() 和销售成本
和销售成本![]() 与
与![]() 的函数关系式
的函数关系式
(2)指出两图象的交点![]() 的实际意义,公司的销售量至少要达到多少才能不亏损?
的实际意义,公司的销售量至少要达到多少才能不亏损?
(3)如果该公司要盈利1万元,需要销售多少吨产品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)请你判断AE、AF与BE之间的数量关系,并说明理由.
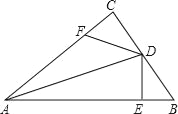
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,
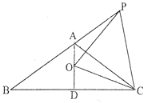
(1)求∠APO+∠DCO的度数;
(2)求证:点P在OC的垂直平分线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com