
【题目】如图,L1反映了某公司产品的销售收入![]() (元)与销售量
(元)与销售量![]() 的函数关系,L2反映了该公司产品的销售成本
的函数关系,L2反映了该公司产品的销售成本![]() (元)与销售量
(元)与销售量![]() 的函数关系,根据图象解答问题:
的函数关系,根据图象解答问题:
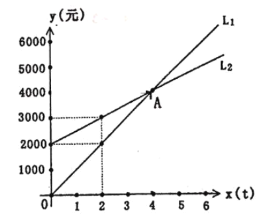
(1)分别求出销售收入![]() 和销售成本
和销售成本![]() 与
与![]() 的函数关系式
的函数关系式
(2)指出两图象的交点![]() 的实际意义,公司的销售量至少要达到多少才能不亏损?
的实际意义,公司的销售量至少要达到多少才能不亏损?
(3)如果该公司要盈利1万元,需要销售多少吨产品?
【答案】(1)![]() ,
,![]() ;(2)交点A的实际意义是销售收入等于销售成本,即不盈利也不亏损;公司的销售量至少要达到4t才能不亏损;(3)如果该公司要盈利1万元,需要销售24吨产品.
;(2)交点A的实际意义是销售收入等于销售成本,即不盈利也不亏损;公司的销售量至少要达到4t才能不亏损;(3)如果该公司要盈利1万元,需要销售24吨产品.
【解析】
(1)分别利用待定系数法求![]() 与
与![]() 的函数关系式即可;
的函数关系式即可;
(2)由![]() 表示销售收入,
表示销售收入,![]() 表示销售成本可知交点A的实际意义是销售收入等于销售成本,即不盈利也不亏损;求出交点横坐标,根据函数图象可得到何时不亏损;
表示销售成本可知交点A的实际意义是销售收入等于销售成本,即不盈利也不亏损;求出交点横坐标,根据函数图象可得到何时不亏损;
(3)根据“盈利=销售收入-销售成本”列式计算即可.
解:(1)设![]() ,
,
由函数图象得:![]() 过点(2,2000),则
过点(2,2000),则![]() ,
,
解得:![]() ,
,
∴![]() ;
;
设![]() ,
,
由函数图象得:![]() 过点(0,2000),(2,3000),则
过点(0,2000),(2,3000),则![]() ,
,
解得:![]() ,
,
∴![]() ;
;
(2)由题意得:交点A的实际意义是销售收入等于销售成本,即不盈利也不亏损;
当![]() 时,即
时,即![]() ,
,
解得:x=4,即A点横坐标为4,
由函数图象可得,当x≥4时,![]() ,
,
∴公司的销售量至少要达到4t才能不亏损;
(3)由题意得:![]() ,即
,即![]() ,
,
解得:![]() ,
,
答:如果该公司要盈利1万元,需要销售24吨产品.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:初中数学 来源: 题型:
【题目】已知∠MON=20° ,点A B分别是射线OM、ON上的动点(A、B不与点0重合),若AB![]() OM,在射线ON上有一点C,设∠OAC=x°,下列x的值不能使△ABC为等腰三角形的是( )
OM,在射线ON上有一点C,设∠OAC=x°,下列x的值不能使△ABC为等腰三角形的是( )
A.20
B.45
C.50
D.125
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,在平面直角坐标系中,点M是二次函数![]() 图象上一点,过点M作
图象上一点,过点M作![]() 轴,如果二次函数
轴,如果二次函数![]() 的图象与
的图象与![]() 关于l成轴对称,则称
关于l成轴对称,则称![]() 是
是![]() 关于点M的伴随函数
关于点M的伴随函数![]() 如图2,在平面直角坐标系中,二次函数
如图2,在平面直角坐标系中,二次函数![]() 的函数表达式是
的函数表达式是![]() ,点M是二次函数
,点M是二次函数![]() 图象上一点,且点M的横坐标为m,二次函数
图象上一点,且点M的横坐标为m,二次函数![]() 是
是![]() 关于点M的伴随函数.
关于点M的伴随函数.



![]() 若
若![]() ,
,
![]() 求
求![]() 的函数表达式.
的函数表达式.
![]() 点
点![]() ,
,![]() 在二次函数
在二次函数![]() 的图象上,若
的图象上,若![]() ,a的取值范围为______.
,a的取值范围为______.
![]() 过点M作
过点M作![]() 轴,
轴,
![]() 如果
如果![]() ,线段MN与
,线段MN与![]() 的图象交于点P,且MP:
的图象交于点P,且MP:![]() :3,求m的值.
:3,求m的值.
![]() 如图3,二次函数
如图3,二次函数![]() 的图象在MN上方的部分记为
的图象在MN上方的部分记为![]() ,剩余的部分沿MN翻折得到
,剩余的部分沿MN翻折得到![]() ,由
,由![]() 和
和![]() 所组成的图象记为
所组成的图象记为![]() .以
.以![]() 、
、![]() 为顶点在x轴上方作正方形
为顶点在x轴上方作正方形![]() 直接写出正方形ABCD与G有三个公共点时m的取值范围.
直接写出正方形ABCD与G有三个公共点时m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
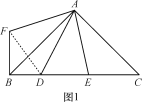
【题目】(1)如图1,△ABC中,∠BAC=90°,AB=AC,D,E在BC上,∠DAE=45°,为了探究BD,DE,CE之间的等量关系,现将△AEC绕A顺时针旋转90°后成△AFB,连接DF,经探究,你所得到的BD,DE,CE之间的等量关系式是 ;(无须证明)
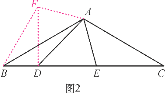
(2)如图2,在△ABC中,∠BAC=120°,AB=AC,D,E在BC上,∠DAE=60°,∠ADE=45°,试仿照(1)的方法,利用图形的旋转变换,探究BD,DE,CE之间的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其顶点为D.

(1)抛物线及直线AC的函数关系式;
(2)设点M(3,m),求使MN+MD的值最小时m的值;
(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;
(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
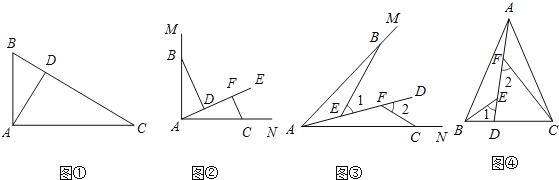
【题目】问题情境:如图①,在直角三角形ABC中,∠BAC=90,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
(1)特例探究:如图②,∠MAN=90,射线AE在这个角的内部,点B.C在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;
(2)归纳证明:如图③,点B,C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)拓展应用:如图④,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E.F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为18,求△ACF与△BDE的面积之和是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
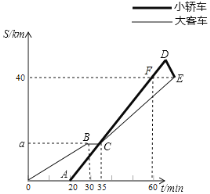
【题目】初二![]() 班同学从学校出发去某自然保护区研学旅行,一部分乘坐大客车先出发,余下的几人20分钟后乘坐小轿车沿同一路线出行
班同学从学校出发去某自然保护区研学旅行,一部分乘坐大客车先出发,余下的几人20分钟后乘坐小轿车沿同一路线出行![]() 大客车中途停车等候,小轿车赶上来之后,大客车以出发时速度的
大客车中途停车等候,小轿车赶上来之后,大客车以出发时速度的![]() 继续行驶,小轿车保持原速度不变
继续行驶,小轿车保持原速度不变![]() 小轿车司机因路线不熟错过了景点入口,再原路提速返回,恰好与大客车同时到达景点入口
小轿车司机因路线不熟错过了景点入口,再原路提速返回,恰好与大客车同时到达景点入口![]() 两车距学校的路程
两车距学校的路程![]() 单位:千米
单位:千米![]() 和行驶时间
和行驶时间![]() 单位:分钟
单位:分钟![]() 之间的函数关系如图所示.
之间的函数关系如图所示.
请结合图象解决下面问题:
![]() 学校到景点的路程为______千米,大客车途中停留了______分钟,
学校到景点的路程为______千米,大客车途中停留了______分钟,![]() ______千米;
______千米;
![]() 在小轿车司机驶过景点入口时,大客车离景点入口还有多远?
在小轿车司机驶过景点入口时,大客车离景点入口还有多远?
![]() 若大客车一直以出发时的速度行驶,中途不再停车,那么小轿车折返后到达景点入口,需等待______分钟,大客车才能到达景点入口.
若大客车一直以出发时的速度行驶,中途不再停车,那么小轿车折返后到达景点入口,需等待______分钟,大客车才能到达景点入口.
查看答案和解析>>
科目:初中数学 来源: 题型:
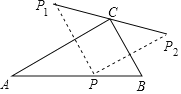
【题目】如图,△ABC中,∠ACB=90°,∠A=30°,AC=6,点P在边AB上运动(不与端点重合),点P关于直线AC,BC对称的点分别为P1,P2.则在点P的运动过程中,线段P1P2的长度m的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某庄有甲、乙两家草莓采摘园的草莓销售价格相同,春节期间,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为![]() (千克),在甲园所需总费用为
(千克),在甲园所需总费用为![]() (元),在乙园所需总费用为
(元),在乙园所需总费用为![]() (元),
(元),![]() 、
、![]() 与
与![]() 之间的函数关系如图所示.
之间的函数关系如图所示.

(1)甲采摘园的门票是_____元,两个采摘园优惠前的草莓单价是每千克____元;
(2)当![]() 时,求
时,求![]() 与
与![]() 的函数表达式;
的函数表达式;
(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com