
����Ŀ����ͼ����֪������y=��x2+bx+c��һֱ���ཻ��A����1��0����C��2��3�����㣬��y�ύ�ڵ�N���䶥��ΪD��

��1��������ֱ��AC�ĺ�����ϵʽ��
��2�����M��3��m������ʹMN+MD��ֵ��Сʱm��ֵ��
��3���������ߵĶԳ�����ֱ��AC�ཻ�ڵ�B��EΪֱ��AC�ϵ�����һ�㣬����E��EF��BD���������ڵ�F����B��D��E��FΪ������ı����ܷ�Ϊƽ���ı��Σ����ܣ����E�����ꣻ�����ܣ���˵�����ɣ�
��4����P����������λ��ֱ��AC�Ϸ���һ�����㣬����APC����������ֵ��
���𰸡���1��![]() ��ֱ��AC�ĺ�����ϵʽΪy=x+1��2��
��ֱ��AC�ĺ�����ϵʽΪy=x+1��2��![]() ��3����2��3������0��1����
��3����2��3������0��1����![]() ��
��![]() ����4��
����4��![]()
��������
�⣺��1����������y=��x2+bx+c����A����1��0����C��2��3���ã�
![]() �����
�����![]() ���������ߵĺ�����ϵʽΪ
���������ߵĺ�����ϵʽΪ![]() ��
��
��ֱ��AC�ĺ�����ϵʽΪy=kx+n����ֱ��AC����A����1��0����C��2��3����
![]() �����
�����![]() ����ֱ��AC�ĺ�����ϵʽΪy=x+1��
����ֱ��AC�ĺ�����ϵʽΪy=x+1��
��2����N�����ֱ��x=3�ĶԳƵ�N����
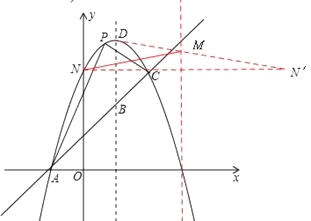
��x=0����y=3����N��0��3����
��N����6�� 3��
��![]() ��
��
D��1��4����
��ֱ��DN���ĺ�����ϵʽΪy=sx+t����
![]() �����
�����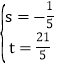 ��
��
����ֱ��DN���ĺ�����ϵʽΪ![]() ��
��
������ԳƵ����ʺ����������߹�ϵ��֪��M��3��m����ֱ��DN����ʱ��MN+MD��ֵ��С��
��![]() ��
��
��ʹMN+MD��ֵ��Сʱm��ֵΪ![]() ��
��
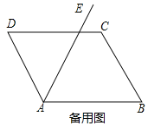
��3���ɣ�1������2����D��1��4����B��1��2����
����BDΪƽ���ı��ζԽ���ʱ����B��C��D��N������֪���ı���BCDN��ƽ���ı��Σ���ʱ����E���C�غϣ���E��2��3����
����BDΪƽ���ı��α�ʱ��
����E��ֱ��AC�ϣ�����E��x��x+1������F��x��![]() ����
����
����BD=2
�����ı���BDEF��BDFE��ƽ���ı���ʱ��BD=EF��
��![]() ����
����![]() ��
��
��![]() ����ã�x=0��x=1����ȥ������E��0��1����
����ã�x=0��x=1����ȥ������E��0��1����
��![]() ����ã�
����ã�![]() ����E
����E![]() ��E
��E![]() ��
��
���ϣ����������ĵ�EΪ��2��3������0��1����![]() ��
��![]() ��
��
��4����ͼ������P��PQ��x�ύAC�ڵ�Q������C��CG��x���ڵ�G��
��Q��x��x+1������P��x����x2+2x+3����
��![]() ��
��
��![]()
![]() ��
��
��![]() ��
��
����![]() ʱ����APC�����ȡ�����ֵ�����ֵΪ
ʱ����APC�����ȡ�����ֵ�����ֵΪ![]() ��
��
��1�����ô���ϵ��������κ�������ʽ��һ�κ�������ʽ��
��2��������ԳƵ����ʺ����������߹�ϵ��N�����ֱ��x=3�ĶԳƵ�N������M��3��m����ֱ��DN����ʱ��MN+MD��ֵ��С��
��3����BDΪƽ���ı��ζԽ��ߺ�BDΪƽ���ı��α�����������ۡ�
��4����ͼ������P��PQ��x�ύAC�ڵ�Q������C��CG��x���ڵ�G����Q��x��x+1������P��x����x2+2x+3��������߶�PQ=��x2+x+2����ͼʾ�Լ������ε������ʽ֪![]() ���ɶ��κ�������ֵ����֪��APC����������ֵ��
���ɶ��κ�������ֵ����֪��APC����������ֵ��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
�У�![]() ���ҵ�
���ҵ�![]() ������Ϊ
������Ϊ![]() ����
����![]() ����Ϊ
����Ϊ![]() ����
����![]() ��
��![]() ��ĸ������ϣ�������
��ĸ������ϣ�������![]() ������
������![]() �͵�
�͵�![]()

![]() ��
��![]() ��
��![]() ��ֵ��
��ֵ��
![]() �������ߵĶԳ������Ƿ���ڵ�
�������ߵĶԳ������Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() Ϊ���������Σ������ڣ�ֱ��д����
Ϊ���������Σ������ڣ�ֱ��д����![]() �����ꣻ�������ڣ���˵������
�����ꣻ�������ڣ���˵������
![]() ��
��![]() ���߶�
���߶�![]() �ϵ�һ�����㣬����
�ϵ�һ�����㣬����![]() ��
��![]() ���ƽ���߽��������ڵ�
���ƽ���߽��������ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ��̽��������
��̽��������![]() ��ʲôλ��ʱ���ı���
��ʲôλ��ʱ���ı���![]() ��ƽ���ı��Σ���ʱ�����ж��ı���
��ƽ���ı��Σ���ʱ�����ж��ı���![]() ����״����˵�����ɣ�
����״����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��չѧ���ĺ�������������ѧ�����ۺ�������ijѧУ�ƻ���������ѡ�Σ��������赸���滭���鷨��ѧУ��ȡ��������ķ��������ʾ�����![]() ÿ���������ѧ������ѡ�����ֻ��ѡ������һ��
ÿ���������ѧ������ѡ�����ֻ��ѡ������һ��![]() �Ե������������������Ƴ�����������������ͳ��ͼ
�Ե������������������Ƴ�����������������ͳ��ͼ![]() ����ͼ��������Ϣ����������⣺
����ͼ��������Ϣ����������⣺


![]() ���ε����ѧ������______�ˣ�������ͳ��ͼ�У�m��ֵ��______��
���ε����ѧ������______�ˣ�������ͳ��ͼ�У�m��ֵ��______��
![]() �ֱ�����μӵ����ѧ����ѡ��滭���鷨����������������ͳ��ͼ����������
�ֱ�����μӵ����ѧ����ѡ��滭���鷨����������������ͳ��ͼ����������
![]() ��У����ѧ��2000�ˣ����Ƹ�УԼ�ж�����ѡ�������γ̣�
��У����ѧ��2000�ˣ����Ƹ�УԼ�ж�����ѡ�������γ̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ũ��ƻ�������������εĹ��ڣ�Ϊ�˱���ƻ�������ܷ紵������ƻ��������Χ������Ҷ��������ͼ�����Կ���ũ������ֲƻ����������(n)��ƻ������������Ҷ�������Ĺ��ɣ���nΪijһ����ֵʱ��ƻ���������������Ҷ����������nΪ___________

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڳ�����![]() �У�BC=3������
��BC=3������![]() ��
��![]() ��������ÿ��1����λ���ٶȣ�������
��������ÿ��1����λ���ٶȣ�������![]() �����ƶ�����
�����ƶ�����![]() ����ֱ��
����ֱ��![]() �ĶԳ�
�ĶԳ�![]() �����
�����![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]()
��1����P�����߶�BC���Ҳ���C���غ�ʱ����ֱ��PB����ֱ��CD�ཻ�ڵ�M���ҡ�PAM=45��������AB�ij�
��2����AB=4
����ͼ2������B������AC��ʱ����Ȼ��PCB����ֱ�������Σ����ʱt��ֵ
���Ƿ��������ͼ2��ʱ�̣�ʹ����PCB����ֱ�������Σ������ڣ���ֱ��д�����з��������t��ֵ���������ڣ���˵������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��L1��ӳ��ij��˾��Ʒ����������![]() ��Ԫ����������
��Ԫ����������![]() �ĺ�����ϵ��L2��ӳ�˸ù�˾��Ʒ�����۳ɱ�
�ĺ�����ϵ��L2��ӳ�˸ù�˾��Ʒ�����۳ɱ�![]() ��Ԫ����������
��Ԫ����������![]() �ĺ�����ϵ������ͼ�������⣺
�ĺ�����ϵ������ͼ�������⣺
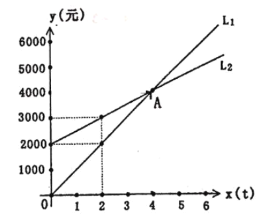
��1���ֱ������������![]() �����۳ɱ�
�����۳ɱ�![]() ��
��![]() �ĺ�����ϵʽ
�ĺ�����ϵʽ
��2��ָ����ͼ��Ľ���![]() ��ʵ�����壬��˾������������Ҫ�ﵽ���ٲ��ܲ�����
��ʵ�����壬��˾������������Ҫ�ﵽ���ٲ��ܲ�����
��3������ù�˾Ҫӯ��1��Ԫ����Ҫ���۶��ٶֲ�Ʒ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
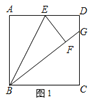
����Ŀ����ͼ1������ABCD�У�![]() ��
��![]() ��
��![]() ������AEƽ��
������AEƽ��![]() ����P��
����P��![]() ���ٶ���AD���յ�D�˶�������P��
���ٶ���AD���յ�D�˶�������P��![]() ��AE�ڵ�Q������P��
��AE�ڵ�Q������P��![]() ������Q��
������Q��![]() ����PM�ڵ�
����PM�ڵ�![]() ���P���˶�ʱ��Ϊ
���P���˶�ʱ��Ϊ![]() ���ı���APMQ���ı���ABCD�ص��������Ϊ
���ı���APMQ���ı���ABCD�ص��������Ϊ![]()


![]() ______
______![]() �ú�t�Ĵ���ʽ��ʾ
�ú�t�Ĵ���ʽ��ʾ![]()
![]() ����M����CD��ʱ����t��ֵ��
����M����CD��ʱ����t��ֵ��
![]() ��S��t֮��ĺ�����ϵʽ��
��S��t֮��ĺ�����ϵʽ��
![]() ��ͼ2������AM����PQ�ڵ�G������AC��BD���ڵ�H��ֱ��д��tΪ��ֵʱ��GH��������ABD��һ��ƽ�л��ߣ�
��ͼ2������AM����PQ�ڵ�G������AC��BD���ڵ�H��ֱ��д��tΪ��ֵʱ��GH��������ABD��һ��ƽ�л��ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() ��ͼ
��ͼ![]() ��������
��������![]() �ı߳�Ϊ
�ı߳�Ϊ![]() ����
����![]() ��
��![]() �ߵ��е㣬��
�ߵ��е㣬��![]() ��
��![]() ���۵õ�
���۵õ�![]() ���ӳ�
���ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() �������ʱ
�������ʱ![]() ��ֵ��
��ֵ��
![]() ��ͼ
��ͼ![]() ������
������![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() �ߵ��е㣬ͬ����
�ߵ��е㣬ͬ����![]() ��
��![]() ���۵õ�
���۵õ�![]() ���ӳ�
���ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
��֤����![]() ��
��
������![]() ǡ��
ǡ��![]() �ߵ��е㣬��
�ߵ��е㣬��![]() ��ֵ��
��ֵ��
����![]() ��
��![]() ���ƣ���
���ƣ���![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �Ǿ���
�Ǿ���![]() ��һ�㣬
��һ�㣬![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��

![]() ���ж��ı���
���ж��ı���![]() �Ƿ��������Σ����ǣ�д��֤�����̣������ǣ�˵�����ɣ�
�Ƿ��������Σ����ǣ�д��֤�����̣������ǣ�˵�����ɣ�
![]() �ӳ�
�ӳ�![]() ����
����![]() ��ʹ
��ʹ![]() ������
������![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ����
����![]() �Ķ�����
�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com