
ЁОЬтФПЁПШчЭМ1ЃЌдкГЄЗНаЮ![]() жаЃЌBC=3ЃЌЖЏЕу
жаЃЌBC=3ЃЌЖЏЕу![]() Дг
Дг![]() ГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШЃЌбиЩфЯп
ГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШЃЌбиЩфЯп![]() ЗНЯђвЦЖЏЃЌзї
ЗНЯђвЦЖЏЃЌзї![]() ЙигкжБЯп
ЙигкжБЯп![]() ЕФЖдГЦ
ЕФЖдГЦ![]() ЃЌЩшЕу
ЃЌЩшЕу![]() ЕФдЫЖЏЪБМфЮЊ
ЕФдЫЖЏЪБМфЮЊ![]()
ЃЈ1ЃЉЕБPЕудкЯпЖЮBCЩЯЧвВЛгыCЕужиКЯЪБЃЌШєжБЯпPBЁЏгыжБЯпCDЯрНЛгкЕуMЃЌЧвЁЯPAM=45ЁуЃЌЪдЧѓЃКABЕФГЄ
ЃЈ2ЃЉШєAB=4
ЂйШчЭМ2ЃЌЕБЕуBЁЏТфдкACЩЯЪБЃЌЯдШЛЁїPCBЁЏЪЧжБНЧШ§НЧаЮЃЌЧѓДЫЪБtЕФжЕ
ЂкЪЧЗёДцдквьгкЭМ2ЕФЪБПЬЃЌЪЙЕУЁїPCBЁЏЪЧжБНЧШ§НЧаЮЃПШєДцдкЃЌЧыжБНгаДГіЫљгаЗћКЯЬтвтЕФtЕФжЕЃПШєВЛДцдкЃЌЧыЫЕУїРэгЩ

ЁОД№АИЁПЃЈ1ЃЉABЕФГЄЮЊ3ЃЛЃЈ2ЃЉЂй![]() ЃЛЂкtЕФжЕЮЊ
ЃЛЂкtЕФжЕЮЊ![]() Лђ
Лђ![]() Лђ4.
Лђ4.
ЁОНтЮіЁП
ЃЈ1ЃЉШчЭМЫљЪОЃЌбгГЄ![]() гыCDНЛгкMЃЌСЌНгAMЃЌгУНЧНЧБпжЄУї
гыCDНЛгкMЃЌСЌНгAMЃЌгУНЧНЧБпжЄУї![]() ЃЌПЩЭЦГіAB=BC=3.
ЃЌПЩЭЦГіAB=BC=3.
ЃЈ2ЃЉЂйдкRtЁї![]() жаЃЌевГіБпГЄРћгУЙДЙЩЖЈРэНЈСЂЗНГЬЧѓНтЃЛ
жаЃЌевГіБпГЄРћгУЙДЙЩЖЈРэНЈСЂЗНГЬЧѓНтЃЛ
ЂкЗжШ§жжЧщПіЬжТлЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЗжБ№зїГіЯргІЕФЭМаЮЃЌдк
ЃЌЗжБ№зїГіЯргІЕФЭМаЮЃЌдк![]() жаЃЌЗжБ№евГіБпГЄЃЌРћгУЙДЙЩЖЈРэНЈСЂЗНГЬЧѓНт.
жаЃЌЗжБ№евГіБпГЄЃЌРћгУЙДЙЩЖЈРэНЈСЂЗНГЬЧѓНт.
ЃЈ1ЃЉШчЭМЫљЪОЃЌбгГЄ![]() гыCDНЛгкMЃЌСЌНгAMЃЌ
гыCDНЛгкMЃЌСЌНгAMЃЌ

гЩелЕўЕФаджЪПЩжЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]()
дк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ

Ёр![]() Ёе
Ёе![]() ЃЈAASЃЉ
ЃЈAASЃЉ
Ёр![]()
гжЁпABCDЮЊОиаЮЃЌЁрAD=BC=3ЃЌ
ЁрAB=3
ЃЈ2ЃЉЂйдкRtЁїABCжаЃЌ![]()
ЁпЕуPЕуЕФдЫЖЏЪБМфЮЊtЃЌЫйЖШЮЊ1ЃЌЁрBP=tЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ,
,
дкRtЁї![]() жаЃЌгЩЙДЙЩЖЈРэга
жаЃЌгЩЙДЙЩЖЈРэга![]() ЃЌМД
ЃЌМД![]() ЃЌНтЕУ
ЃЌНтЕУ![]() .
.
ЂкЕБ![]() ЃЌШчЯТЭМЫљЪОЃЌ
ЃЌШчЯТЭМЫљЪОЃЌ

ЁпЫФБпаЮABCDЮЊОиаЮЃЌЁрAD=BC=3ЃЌCD=AB=4ЃЌ
гаелЕўаджЪга![]() ЃЌдкRtЁї
ЃЌдкRtЁї![]() жаЃЌ
жаЃЌ
![]() ЃЌ
ЃЌ
Ёр![]()
дкRtЁї![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]()
![]() ЃЌМД
ЃЌМД![]() ЃЌНтЕУ
ЃЌНтЕУ![]()
ЕБЁЯ![]() =90ЁуЪБЃЌШчЯТЭМЫљЪОЃЌ
=90ЁуЪБЃЌШчЯТЭМЫљЪОЃЌ

гЩелЕўПЩЕУ![]() ЃЌ
ЃЌ
дкRtЁї![]() жаЃЌ
жаЃЌ![]()
дкRtЁї![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
![]() ЃЌМД
ЃЌМД![]() ЃЌНтЕУ
ЃЌНтЕУ![]()
ЕБ![]() =90ЁуЪБЃЌШчЯТЭМЫљЪОЃЌИљОнелЕўвзЕУЫФБпаЮ
=90ЁуЪБЃЌШчЯТЭМЫљЪОЃЌИљОнелЕўвзЕУЫФБпаЮ![]() ЮЊе§ЗНаЮЃЌЁрPB=AB=4
ЮЊе§ЗНаЮЃЌЁрPB=AB=4

злЩЯЃЌТњзуЬтвтЕФtЕФжЕЮЊ![]() Лђ
Лђ![]() Лђ4.
Лђ4.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуE, FдкжБЯпACЩЯЃЌDF=BEЃЌ ЁЯAFD=ЁЯCEB,ЯТСаЬѕМўжаВЛФмХаЖЯЁїADFЁеЁїCBEЕФЪЧ( )

A.ЁЯD=ЁЯBB.AD=CBC.AE=CFD.AD// BC
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯACBЃН90ЁуЃЌЙ§ЕуCзїCDЁЭABгкDЃЌЁЯAЃН30ЁуЃЌBDЃН1ЃЌдђABЕФжЕЪЧЃЈЁЁЁЁЃЉ.
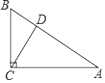
A.1B.2C.3D.4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋЦНааЫФБпаЮжНЦЌABCDАДШчЭМЗНЪНелЕўЃЌЪЙЕуCгыAжиКЯЃЌЕуDТфЕНDЁфДІЃЌелКлЮЊEFЃЎ

ЃЈ1ЃЉЧѓжЄЃКЁїABEЁеЁїADЁфFЃЛ
ЃЈ2ЃЉСЌНгCFЃЌХаЖЯЫФБпаЮAECFЪЧЪВУДЬиЪтЫФБпаЮЃПжЄУїФуЕФНсТлЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
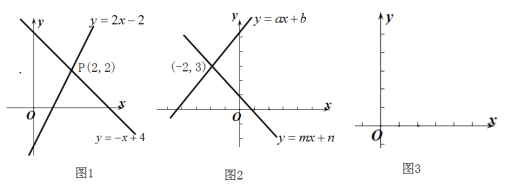
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯп![]() ЪЧЕквЛЁЂШ§ЯѓЯоЕФНЧЦНЗжЯп.
ЪЧЕквЛЁЂШ§ЯѓЯоЕФНЧЦНЗжЯп.

ЃЈ1ЃЉгЩЭМЙлВьвзжЊAЃЈ0ЃЌ2ЃЉЙигкжБЯпlЕФЖдГЦЕуAЁфЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЌЧыдкЭМжаЗжБ№БъУїBЃЈ5ЃЌ3ЃЉЁЂCЃЈ-2ЃЌ5ЃЉЙигкжБЯпlЕФЖдГЦЕуBЁфЁЂCЁфЕФЮЛжУЃЌВЂаДГіЫћУЧЕФзјБъЃК![]() ___________ЁЂ
___________ЁЂ![]() ___________ЃЛ
___________ЃЛ
ЃЈ2ЃЉНсКЯЭМаЮЙлВьвдЩЯШ§зщЕуЕФзјБъЃЌФуЛсЗЂЯжЃКзјБъЦНУцФкШЮвЛЕу![]() ЙигкЕквЛЁЂШ§ЯѓЯоЕФНЧЦНЗжЯп
ЙигкЕквЛЁЂШ§ЯѓЯоЕФНЧЦНЗжЯп![]() ЕФЖдГЦЕу
ЕФЖдГЦЕу![]() ЕФзјБъЮЊ___________ЃЈВЛБижЄУїЃЉЃЛ
ЕФзјБъЮЊ___________ЃЈВЛБижЄУїЃЉЃЛ
ЃЈ3ЃЉвбжЊСНЕу![]() ЁЂ
ЁЂ![]() ЃЌЪддкжБЯпLЩЯЛГіЕуQЃЌЪЙЕуQЕНDЁЂEСНЕуЕФОрРыжЎКЭзюаЁЃЌЧѓQD+QEЕФзюаЁжЕЃЎ
ЃЌЪддкжБЯпLЩЯЛГіЕуQЃЌЪЙЕуQЕНDЁЂEСНЕуЕФОрРыжЎКЭзюаЁЃЌЧѓQD+QEЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпy=Љx2+bx+cгывЛжБЯпЯрНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌCЃЈ2ЃЌ3ЃЉСНЕуЃЌгыyжсНЛгкЕуNЃЎЦфЖЅЕуЮЊDЃЎ

ЃЈ1ЃЉХзЮяЯпМАжБЯпACЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЩшЕуMЃЈ3ЃЌmЃЉЃЌЧѓЪЙMN+MDЕФжЕзюаЁЪБmЕФжЕЃЛ
ЃЈ3ЃЉШєХзЮяЯпЕФЖдГЦжсгыжБЯпACЯрНЛгкЕуBЃЌEЮЊжБЯпACЩЯЕФШЮвтвЛЕуЃЌЙ§ЕуEзїEFЁЮBDНЛХзЮяЯпгкЕуFЃЌвдBЃЌDЃЌEЃЌFЮЊЖЅЕуЕФЫФБпаЮФмЗёЮЊЦНааЫФБпаЮЃПШєФмЃЌЧѓЕуEЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ4ЃЉШєPЪЧХзЮяЯпЩЯЮЛгкжБЯпACЩЯЗНЕФвЛИіЖЏЕуЃЌЧѓЁїAPCЕФУцЛ§ЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЁЂЫМПМЁЂНтОіЮЪЬтЃК
ЃЈ1ЃЉШчЭМЃЈ1ЃЉСНИіКЏЪ§![]() КЭ
КЭ![]() ЕФЭМЯѓНЛгкЕу
ЕФЭМЯѓНЛгкЕу![]() ЃЌ
ЃЌ![]() ЕФзјБъ
ЕФзјБъ![]() ЪЧЗёТњзуетСНИіКЏЪ§ЪНЃПМД
ЪЧЗёТњзуетСНИіКЏЪ§ЪНЃПМД![]() ЪЧЗНГЬ
ЪЧЗНГЬ![]() ЕФНтТ№ЃПЪЧЗНГЬ
ЕФНтТ№ЃПЪЧЗНГЬ![]() ЕФНтТ№ЃПД№ЃК Ђй ЃЈЪЧЁЂВЛЪЧЃЉетОЭЪЧЫЕЃККЏЪ§
ЕФНтТ№ЃПД№ЃК Ђй ЃЈЪЧЁЂВЛЪЧЃЉетОЭЪЧЫЕЃККЏЪ§![]() КЭ
КЭ![]() ЭМЯѓЕФНЛЕузјБъ Ђк ЃЈЪЧЁЂВЛЪЧЃЉЗНГЬзщ
ЭМЯѓЕФНЛЕузјБъ Ђк ЃЈЪЧЁЂВЛЪЧЃЉЗНГЬзщ![]() ЕФНтЃЛЗДжЎЃЌЗНГЬзщ
ЕФНтЃЛЗДжЎЃЌЗНГЬзщ![]() ЕФНт Ђл ЃЈЪЧЁЂВЛЪЧЃЉКЏЪ§
ЕФНт Ђл ЃЈЪЧЁЂВЛЪЧЃЉКЏЪ§![]() КЭ
КЭ![]() ЭМЯѓЕФНЛЕузјБъЃЎ
ЭМЯѓЕФНЛЕузјБъЃЎ
ЃЈ2ЃЉИљОнЭМЃЈ2ЃЉаДГіЗНГЬзщ![]() ЕФНтЪЧЃК____________
ЕФНтЪЧЃК____________
ЃЈ3ЃЉвбжЊСНИівЛДЮКЏЪ§![]() КЭ
КЭ![]() ЃЎ
ЃЎ
ЂйЧѓетСНИіКЏЪ§ЭМЯѓЕФНЛЕузјБъЃЛ
ЂкдкЭМЃЈ3ЃЉЕФзјБъЯЕжаЛГіетСНИіКЏЪ§ЕФЭМЯѓ
ЂлИљОнЭМЯѓаДГіЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫФБпаЮABCDжаЃЌЁЯA=140ЁуЃЌЁЯD=80Ёу.

(1)ШчЭМ1ЃЌШєЁЯB=ЁЯCЃЌЪдЧѓГіЁЯCЕФЖШЪ§ЃЛ
(2)ШчЭМ2ЃЌШєЁЯABCЕФНЧЦНЗжЯпBEНЛDCгкЕуEЃЌЧвBEЁЮADЃЌЪдЧѓГіЁЯCЕФЖШЪ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯCЃН90ЁуЃЌRtЁїBAPжаЃЌЁЯBAPЃН90ЁуЃЌвбжЊЁЯCBOЃНЁЯABPЃЌBPНЛACгкЕуOЃЌEЮЊACЩЯвЛЕуЃЌЧвAEЃНOC.

(1)ЧѓжЄ:APЃНAO;
(2)ЧѓжЄ:PEЁЭAO.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com