
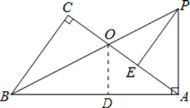
【题目】如图,在Rt△ABC中,∠C=90°,Rt△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.

(1)求证:AP=AO;
(2)求证:PE⊥AO.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据等角的余角相等证明即可;
(2)过点O作OD⊥AB于D,根据角平分线上的点到角的两边的距离相等可得CO=DO,利用“SAS”证明△APE和△OAD全等,根据全等三角形对应角相等可得∠AEP=∠ADO=90°,从而得证.
(1)证明:∵∠C=90°,∠BAP=90°
∴∠CBO+∠BOC=90°,∠ABP+∠APB=90°,
又∵∠CBO=∠ABP,
∴∠BOC=∠APB,
∵∠BOC=∠AOP,
∴∠AOP=∠APB,
∴AP=AO;
(2)证明:如图,过点O作OD⊥AB于D,
∵∠CBO=∠ABP,
∴CO=DO,
∵AE=OC,
∴AE=OD,
∵∠AOD+∠OAD=90°,∠PAE+∠OAD=90°,
∴∠AOD=∠PAE,
在△AOD和△PAE中,
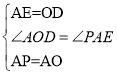 ,
,
∴△AOD≌△PAE(SAS),
∴∠AEP=∠ADO=90°
∴PE⊥AO.


科目:初中数学 来源: 题型:
【题目】如图1,在长方形![]() 中,BC=3,动点
中,BC=3,动点![]() 从
从![]() 出发,以每秒1个单位的速度,沿射线
出发,以每秒1个单位的速度,沿射线![]() 方向移动,作
方向移动,作![]() 关于直线
关于直线![]() 的对称
的对称![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]()
(1)当P点在线段BC上且不与C点重合时,若直线PB’与直线CD相交于点M,且∠PAM=45°,试求:AB的长
(2)若AB=4
①如图2,当点B’落在AC上时,显然△PCB’是直角三角形,求此时t的值
②是否存在异于图2的时刻,使得△PCB’是直角三角形?若存在,请直接写出所有符合题意的t的值?若不存在,请说明理由

查看答案和解析>>
科目:初中数学 来源: 题型:
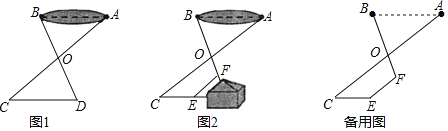
【题目】如图1,为测量池塘宽度AB,可在池塘外的空地上取任意一点O,连接AO,BO,并分别延长至点C,D,使OC=OA,OD=OB,连接CD
(1)求证:AB=CD;
(2)如图2,受地形条件的影响,于是采取以下措施:延长AO至点C,使OC=OA,过点C作AB的平行线CE,延长BO至点F,连接EF,测得∠CEF=140°,∠OFE=110°,CE=11m,EF=10m,请直接写出池塘宽度AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高尔夫球手基础的高尔夫球的运动路线是一条抛物线,当球水平运动了![]() 时达到最高点.落球点比击球点的海拔低
时达到最高点.落球点比击球点的海拔低![]() ,水平距离为
,水平距离为![]() .
.
![]() 建立适当的坐标系,求高度
建立适当的坐标系,求高度![]() 关于水平距离
关于水平距离![]() 的二次函数式;
的二次函数式;
![]() 与击球点相比,运动到最高点时有多高?
与击球点相比,运动到最高点时有多高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】能够判别一个四边形是菱形的条件是( )
A. 一组对角相等且一条对角线平分这组对角 B. 对角线互相平分
C. 对角线互相垂直且相等 D. 对角线相等且互相平分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是矩形
是矩形![]() 内一点,
内一点,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() .
.

![]() 请判断四边形
请判断四边形![]() 是否是正方形?若是,写出证明过程:若不是,说明理由;
是否是正方形?若是,写出证明过程:若不是,说明理由;
![]() 延长
延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利50元。为了尽快减少库存,商场决定采取适当的降价措施。经调查发现,每件商品每降价1元,商场平均每天可多售出2件。设每件商品降价![]() 元。据此规律,请回答:
元。据此规律,请回答:
(1)商场日销售量增加_____件,每件商品盈利_____元(用含![]() 的代数式表示)。
的代数式表示)。
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(a,b)是抛物线![]() 上一动点,OB⊥OA交抛物线于点B(c,d).当点A在抛物线上运动的过程中(点A不与坐标原点O重合),以下结论:①ac为定值;②ac=﹣bd;③△AOB的面积为定值;④直线AB必过一定点.正确的有( )
上一动点,OB⊥OA交抛物线于点B(c,d).当点A在抛物线上运动的过程中(点A不与坐标原点O重合),以下结论:①ac为定值;②ac=﹣bd;③△AOB的面积为定值;④直线AB必过一定点.正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com