
【题目】高尔夫球手基础的高尔夫球的运动路线是一条抛物线,当球水平运动了![]() 时达到最高点.落球点比击球点的海拔低
时达到最高点.落球点比击球点的海拔低![]() ,水平距离为
,水平距离为![]() .
.
![]() 建立适当的坐标系,求高度
建立适当的坐标系,求高度![]() 关于水平距离
关于水平距离![]() 的二次函数式;
的二次函数式;
![]() 与击球点相比,运动到最高点时有多高?
与击球点相比,运动到最高点时有多高?
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案科目:初中数学 来源: 题型:
【题目】将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′处,折痕为EF.

(1)求证:△ABE≌△AD′F;
(2)连接CF,判断四边形AECF是什么特殊四边形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠A=140°,∠D=80°.

(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若△ABC内一点P,满足∠PAB=∠PBC=∠PCA=α,则称点P为△ABC的布洛卡点.通过研究一些特殊三角形中的布洛卡点,得到如下两个结论:
①若∠BAC=90°,则必有∠APC=90°;②若AB=AC,则必有∠APB=∠BPC.
对于这两个结论,下列说法正确的是( )
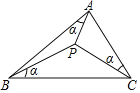
A.①对,②错B.①错,②对C.①,②均错D.①,②均对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动手操作:长为1,宽为a的长方形纸片(![]() <a<l),如图那样折一下,剪下一个边长等于长方形宽度的正方形(称为第一次操作);再把剩下的长方形如图那样折一下,剪下一个边长等于此时长方形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的长方形为正方形,则操作终止.当n=3时,a的值为( )
<a<l),如图那样折一下,剪下一个边长等于长方形宽度的正方形(称为第一次操作);再把剩下的长方形如图那样折一下,剪下一个边长等于此时长方形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的长方形为正方形,则操作终止.当n=3时,a的值为( )
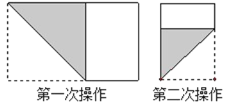
A.![]() B.
B.![]() 或
或![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB,AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为_____.
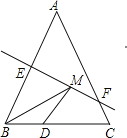
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,Rt△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.

(1)求证:AP=AO;
(2)求证:PE⊥AO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,△ABD是等腰直角三角形,∠BAD=90°,AE⊥BD与点E,连CD分别交AE、AB于点F、G,过点A作AH⊥CD交BD于点H,则下列结论:①∠ADC=15°;②AF=AG;③△ADF≌△BAH;④ DF=2EH,其中正确结论的个数为( )
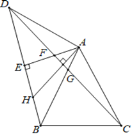
A.4B.3C.2D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com