
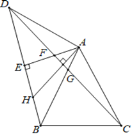
【题目】如图,△ABC是等边三角形,△ABD是等腰直角三角形,∠BAD=90°,AE⊥BD与点E,连CD分别交AE、AB于点F、G,过点A作AH⊥CD交BD于点H,则下列结论:①∠ADC=15°;②AF=AG;③△ADF≌△BAH;④ DF=2EH,其中正确结论的个数为( )
A.4B.3C.2D.1
【答案】B
【解析】
①由等边三角形与等腰直角三角形知△CAD是等腰三角形且顶角∠CAD=150°,据此可判断;②求出∠AFP和∠FAG度数,从而得出∠AGF度数,据此可判断;③根据ASA证明△ADF≌△BAH即可判断③④正确;⑤由∠BAE=45°,∠ADC=∠BAH=15°,则∠EAH=30°,DF=2EH即可得出.
∵△ABC为等边三角形,△ABD为等腰直角三角形,
∴∠BAC=60°、∠BAD=90°、AC=AB=AD,∠ADB=∠ABD=45°,
∴△CAD是等腰三角形,且顶角∠CAD=150°,
∴∠ADC=15°,故①正确;
∵AE⊥BD,即∠AED=90°,
∴∠DAE=45°,
∴∠AFG=∠ADC+∠DAE=60°,∠FAG=45°,
∴∠AGF=75°,
由∠AFG≠∠AGF知AF≠AG,故②错误;
记AH与CD的交点为P,
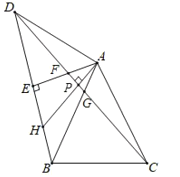
由AH⊥CD且∠AFG=60°知∠FAP=30°,
则∠BAH=∠ADC=15°,
在△ADF和△BAH中,
∵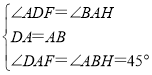 ,
,
∴△ADF≌△BAH(ASA),
∴DF=AH,故③④正确;
∵∠ABE=∠EAB=45°,∠ADF=∠BAH=15°,
∴∠EAH=∠EAB∠BAH=45°15°=30°,
∴AH=2EH,
∴DF=2EH.
故⑤正确.
故选:B.


科目:初中数学 来源: 题型:
【题目】高尔夫球手基础的高尔夫球的运动路线是一条抛物线,当球水平运动了![]() 时达到最高点.落球点比击球点的海拔低
时达到最高点.落球点比击球点的海拔低![]() ,水平距离为
,水平距离为![]() .
.
![]() 建立适当的坐标系,求高度
建立适当的坐标系,求高度![]() 关于水平距离
关于水平距离![]() 的二次函数式;
的二次函数式;
![]() 与击球点相比,运动到最高点时有多高?
与击球点相比,运动到最高点时有多高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利50元。为了尽快减少库存,商场决定采取适当的降价措施。经调查发现,每件商品每降价1元,商场平均每天可多售出2件。设每件商品降价![]() 元。据此规律,请回答:
元。据此规律,请回答:
(1)商场日销售量增加_____件,每件商品盈利_____元(用含![]() 的代数式表示)。
的代数式表示)。
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行.某自行车店在销售某型号自行车时,以高出进价的50%标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)求该型号自行车的进价和标价分别是多少元?
(2)若该型号自行车的进价不变,按(1)中的标价出售,该店平均每月可售出51辆;若每辆自行车每降价20元,每月可多售出3辆,求该型号自行车降价多少元时,每月获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(a,b)是抛物线![]() 上一动点,OB⊥OA交抛物线于点B(c,d).当点A在抛物线上运动的过程中(点A不与坐标原点O重合),以下结论:①ac为定值;②ac=﹣bd;③△AOB的面积为定值;④直线AB必过一定点.正确的有( )
上一动点,OB⊥OA交抛物线于点B(c,d).当点A在抛物线上运动的过程中(点A不与坐标原点O重合),以下结论:①ac为定值;②ac=﹣bd;③△AOB的面积为定值;④直线AB必过一定点.正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=﹣x2+4x+c的图象经过A(1,y1),B(﹣1,y2),C(2+ ![]() ,y3)三点,则y1、y2、y3的大小关系是( )
,y3)三点,则y1、y2、y3的大小关系是( )
A. y1<y2<y3 B. y1<y3<y2 C. y2<y3<y1 D. y2<y1<y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 (1)如图1,等腰Rt△ABC中,∠CAB=90°,点H在BC边上,连AH,作等腰Rt△HFA,∠HFA=90°求证:AF=CF.
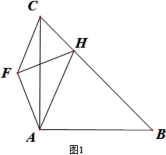
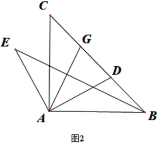
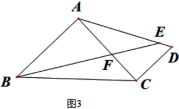
(2)如图2,等腰Rt△ABC中,∠CAB=90°,D在BC上,AD⊥AE,AD=AE,G为CD中点,求证:AG⊥BE
(3)如图3,等腰Rt△ABC中,∠BAC=90°,过C作CD∥AB, CD=8,连AD,在AD上取一点E使AE=AB,连BE交AC于F,若AF=9,则AD= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com