
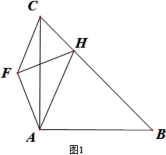
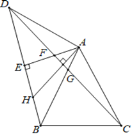
����Ŀ�� (1)��ͼ1������Rt��ABC�У���CAB=90������H��BC���ϣ���AH��������Rt��HFA����HFA=90����֤��AF=CF.
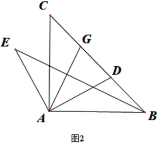
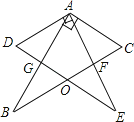
(2)��ͼ2������Rt��ABC�У���CAB=90����D��BC�ϣ�AD��AE,AD=AE,GΪCD�е㣬��֤��AG��BE
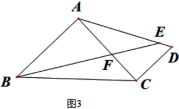
(3)��ͼ3������Rt��ABC�У���BAC=90������C��CD��AB, CD=8����AD,��AD��ȡһ��EʹAE=AB����BE��AC��F����AF=9����AD= .
���𰸡���1������������2������������3��17.
��������
��1����AHΪֱ����ԲO����BC���ڵ�E���ɵá�AEC=90�㣬�ɵ������������ߺ�һ��֪AEΪBC���ϵ����ߣ�����EA=EC������Բ�ܽǶ����Ƴ���AEF=��AHF=45��=��CEF���ٴ��ɵ������������ߺ�һ��֪EF��ֱƽ��AC�����ɵ�֤��
��2���ӳ�AG��N��ʹGN=AG������CN����֤��AGD�ա�NGC��Ȼ���Ƴ���ACN=��BAE����֤����ACN�ա�BAE���õ���CAN=��ABE�����ɵó����ۣ�
��3���ӳ�BE��CD����G����DG=DE����CF=a����AC=AB=AE=AF+CF=9+a�������������ζ�Ӧ�߳ɱ�������a��ʾ��CG��DE��AD��Ȼ���ù��ɶ��������������.
֤������1����ͼ��ʾ����AHΪֱ����ԲO����BC���ڵ�E��

���AEC=90�㣬��AE��BC��
��AB=AC
��AEΪBC���ϵ����ߣ�
��EA=EC
�ɡߡ�AEF=��AHF=45��
���CEF=90��-45��=45��
���AEF=��CEF
�ɵ������������ߺ�һ�ɵ�EF��ֱƽ��AC��
��AF=CF
��2���ӳ�AG��N��ʹGN=AG������CN��
��GΪCD�е㣬
��CG=DG��
�ڡ�AGD�͡�NGC�У�
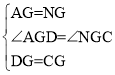
���AGD�ա�NGC��SAS��
���DAG=��N��AD=NC����ADG=��NCG
��AE=AD
��AE=NC
�ߡ�EAC+��CAD=90�㣬��BAD+��CAD=90�㣬
���EAC=��BAD
�ߡ�ADG=��BAD+��ABD=��BAD+45��
���ACN=��NCG+45��=��BAD+90��
�֡ߡ�BAE=��EAC+90��
���ACN=��BAE
�ڡ�ACN�͡�BAE�У�
���ACN�ա�BAE��SAS��
���CAN=��ABE
�֡ߡ�ABE+��AMB=90��
���CAN+��AMB=90��
��AG��BE
��3����ͼ���ӳ�BE��CD����G��

��AB��CD
���ACD=��BAC=90�㣬��G=��ABE
�֡�AB=AE��
���ABE=��AEB��
��AEB=��DEG
���G=��DEG
��DG=DE
��CF=a����AC=AB=AE=AF+CF=9+a
��AB��CD��
���ABF�ס�CGF
��![]() ����
����![]()
���![]()
��DE=DG=CG-CD=![]()
��AD=AE+DE=![]()
��Rt��ACD��AC2+CD2=AD2
��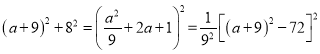
��![]() ����ԭ���̱���Ϊ
����ԭ���̱���Ϊ![]()
������![]() �����x=0��225
�����x=0��225
��![]() ��
��![]()
��ȥ������![]()
��AD=![]()
�ʴ�Ϊ��17.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǵȱ������Σ���ABD�ǵ���ֱ�������Σ���BAD��90����AE��BD���E����CD�ֱ�AE��AB�ڵ�F��G������A��AH��CD��BD�ڵ�H�������н��ۣ��١�ADC��15������AF��AG������ADF�ա�BAH���� DF��2EH��������ȷ���۵ĸ���Ϊ�� ��
A.4B.3C.2D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ȫ��ͬ�ĺ�30����ֱ�����ǰ������һ���ҡ�DAB��30�����������ĸ����ۣ���AF��BC���ڡ�BOE��135������OΪBC�е㣻��AG��DE��1��3��������ȷ���۵�����ǣ�������
A.�٢�B.�ڢ�C.�ڢ�D.�٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijУ�ۺ�ʵ���С���ͬѧ����������һ����DE�ĸ߶ȣ��������������ǰ��һ��¥ͤǰ��̨����A�㴦���������D������Ϊ30��������������ķ����ߵ�̨���µĵ�C�������������D������Ϊ60������֪A��ĸ߶�ABΪ2�ף�̨��AC���¶�Ϊ1��![]() ����AB��BC=1��
����AB��BC=1��![]() ������B��C��E������ͬһ��ֱ���ϣ�������������������DE�ĸ߶ȣ��������ĸ߶Ⱥ��Բ��ƣ���
������B��C��E������ͬһ��ֱ���ϣ�������������������DE�ĸ߶ȣ��������ĸ߶Ⱥ��Բ��ƣ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧ��ѧ��ȤС��Թ���x�ķ��̣�m+1��![]() +��m��2��x��1=0������������⣺
+��m��2��x��1=0������������⣺
��1���Ƿ����m��ֵ��ʹ����ΪһԪ���η��̣������ڣ����m��ֵ������˷��̣�
��2���Ƿ����m��ֵ��ʹ����ΪһԪһ�η��̣������ڣ����m��ֵ������˷��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ�ӿ�ƽ�����ⷽ�̣�
(1) 4(x��2)2��36��0��
(2) x2��6x��9��25��
(3) 4(3x��1)2��9(3x��1)2��0.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��ֱ�������ε�ֽƬ����ֱ�DZ�AC=6cm��BC=8cm���ֽ�ֱ�DZ�AC��ֱ��AD�۵���ʹ������б��AB�ϣ�����AE�غϣ���CD���ڣ����� ��.

A. 2 cm B. 4 cm C. 3 cm D. 5 cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A��˫����y=![]() �ڵ�һ�����ϵ�һ���㣬����AO���ӳ�����һ��֧�ڵ�B����ABΪ�����ȱ�������ABC����C�ڵ������ޣ���֪��C��λ��ʼ����һ����ͼ�����˶����������������ʽΪ��������
�ڵ�һ�����ϵ�һ���㣬����AO���ӳ�����һ��֧�ڵ�B����ABΪ�����ȱ�������ABC����C�ڵ������ޣ���֪��C��λ��ʼ����һ����ͼ�����˶����������������ʽΪ��������

A. y=��![]() B. y=��
B. y=��![]() ��x��0�� C. y=��6x��x��0�� D. y=6x��x��0��
��x��0�� C. y=��6x��x��0�� D. y=6x��x��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B��C��ֱ��l�ϵ������㣬��DAB����DBE����ECB��a����BD��BE��
��1����֤��AC��AD+CE��
��2����a��120������F��ֱ��l���Ϸ�����BEFΪ�ȱ������Σ���ȫͼ�Σ����ж���ACF����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com