
【题目】向阳中学数学兴趣小组对关于x的方程(m+1)![]() +(m﹣2)x﹣1=0提出了下列问题:
+(m﹣2)x﹣1=0提出了下列问题:
(1)是否存在m的值,使方程为一元二次方程?若存在,求出m的值,并解此方程;
(2)是否存在m的值,使方程为一元一次方程?若存在,求出m的值,并解此方程.
【答案】(1)m=1,解得x1=1,x2=﹣![]() ;
;
(2)m=0时解得x=﹣1;m=﹣1时,解得x=﹣![]() .
.
【解析】【试题分析】
(1)根据一元二次方程的定义,要求含有二次项,且二次项系数不为0,即![]() ,解得m=1,将m=1代入(m+1)
,解得m=1,将m=1代入(m+1)![]() +(m﹣2)x﹣1=0,此时方程为2x2-x-1=0,解得x1=1,x2=-
+(m﹣2)x﹣1=0,此时方程为2x2-x-1=0,解得x1=1,x2=-![]() ;
;
(2)根据一元一次方程的定义,要求未知数的最高次为1,该题目分类讨论:当(m+1)![]() 存在的话,则m2+1=1解得m=0,此时方程为-x-1=0,解得x=-1;当(m+1)
存在的话,则m2+1=1解得m=0,此时方程为-x-1=0,解得x=-1;当(m+1)![]() 不存在的话,则m+1=0时,解得m=-1,此时方程为-3x-1=0,解得x=-
不存在的话,则m+1=0时,解得m=-1,此时方程为-3x-1=0,解得x=-![]() .
.
【试题解析】
(1)根据一元二次方程的定义可得![]() ,解得m=1,此时方程为2x2-x-1=0,解得x1=1,x2=-
,解得m=1,此时方程为2x2-x-1=0,解得x1=1,x2=-![]() ;
;
(2)由题可知m2+1=1或m+1=0时方程为一元一次方程
当m2+1=1时,解得m=0,此时方程为-x-1=0,解得x=-1,
当m+1=0时,解得m=-1,此时方程为-3x-1=0,解得x=-![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )
A. (![]() ,0) B. (2,0) C. (
,0) B. (2,0) C. (![]() ,0) D. (3,0)
,0) D. (3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C,D分别在两个半圆上(不与点A、B重合),AD、BD的长分别是关于x的方程![]() =0的两个实数根.
=0的两个实数根.
(1)求m的值;
(2)连接CD,试探索:AC、BC、CD三者之间的等量关系,并说明理由;
(3)若CD=![]() ,求AC、BC的长.
,求AC、BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C、D的坐标分别为A(9,0)、C(0,4),D(5,0),点P从点O出发,以每秒1个单位长度的速度沿O[Math Processing Error] ![]()
![]() C[Math Processing Error]
C[Math Processing Error] ![]()
![]() B[Math Processing Error]
B[Math Processing Error] ![]()
![]() A运动,点P的运动时间为t秒.
A运动,点P的运动时间为t秒.
(1)当t=5时, P点坐标为____________;
(2)当t>4时,OP+PD有最小值吗?如果有,请算出该最小值,如果没有,请说明理由;
(3)当t为何值时,△ODP是腰长为5的等腰三角形?(直接写出t的值).


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例.
原题:如图①,点![]() 分别在正方形
分别在正方形![]() 的边
的边![]() 上,
上, ![]() ,连接
,连接![]() ,则
,则![]() ,试说明理由.
,试说明理由.
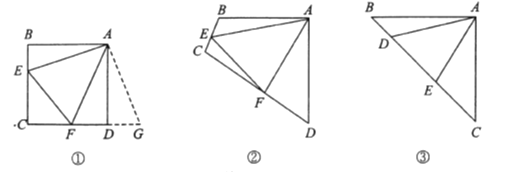
(1)思路梳理
因为![]() ,所以把
,所以把![]() 绕点
绕点![]() 逆时针旋转90°至
逆时针旋转90°至![]() ,可使
,可使![]() 与
与![]() 重合.因为
重合.因为![]() ,所以
,所以![]() ,点
,点![]() 共线.
共线.
根据 ,易证![]() ,得
,得![]() .请证明.
.请证明.
(2)类比引申
如图②,四边形![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 分别在边
分别在边![]() 上,
上, ![]() .若
.若![]() 都不是直角,则当
都不是直角,则当![]() 与
与![]() 满足等量关系时,
满足等量关系时, ![]() 仍然成立,请证明.
仍然成立,请证明.
(3)联想拓展
如图③,在![]() 中,
中, ![]() ,点
,点![]() 均在边
均在边![]() 上,且
上,且![]() .猜想
.猜想![]() 应满足的等量关系,并写出证明过程.
应满足的等量关系,并写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的方格中,每个小正方形的边长都为1,△ABC的顶点均在格点上.在建立平面直角坐标系后,点B的坐标为(﹣1,2).
(1)把△ABC向下平移8个单位后得到对应的△A1B1C1,画出△A1B1C1;
(2)画出与△A1B1C1关于y轴对称的△A2B2C2;
(3)若点P(a,b)是△ABC边上任意一点,P2是△A2B2C2边上与P对应的点,写出P2的坐标为 ;
(4)试在y轴上找一点Q(在图中标出来),使得点Q到B2、C2两点的距离之和最小,并求出QB2+QC2的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC(顶点是网格线的交点)
(1)先将△ABC竖直向上平移5个单位,再水平向右平移4个单位得到△A1B1C1,请画出△A1B1C1;
(2)将△A1B1C1绕B1点顺时针旋转90°,得△A2B1C2,请画出△A2B1C2;
(3)求线段B1C1变换到B1C2的过程中扫过区域的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com