练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】用直接开平方法解方程：

    (1) 4(x－2)2－36＝0；

    (2) x2＋6x＋9＝25；

    (3) 4(3x－1)2－9(3x＋1)2＝0.

    【答案】(1) x1＝5，x2＝－1；（2）x1＝－8，x2＝2；（3）x1＝－，x2＝－

    【解析】试题分析：

    （1）先移项，系数化为1后，再用直接开平方求解；

    （2）左边因式分解为一个完全平方式后，再用直接开平方法求解；

    （3）先移项，再用直接开平方法求解.

    试题解析：

    (1) 4(x－2)2－36＝0，(x－2)2=9，x-2=±3，所以x1＝5，x2＝－1；

    (2) x2＋6x＋9＝25，(x+3)2=25，x+2=±5，所以x1＝－8，x2＝2；

    (3) 4(3x－1)2－9(3x＋1)2＝0，2(3x-1)=±3(3x+1)，所以x1＝－，x2＝－.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，AB=16cm，BC=6cm，点P从点A出发沿AB向点B移动（不与点A、B重合），一直到达点B为止；同时，点Q从点C出发沿CD向点D移动（不与点C、D重合）．运动时间设为t秒．

    （1）若点P、Q均以3cm/s的速度移动，则：AP=　　cm；QC=　　cm．（用含t的代数式表示）

    （2）若点P为3cm/s的速度移动，点Q以2cm/s的速度移动，经过多长时间PD=PQ，使△DPQ为等腰三角形？

    （3）若点P、Q均以3cm/s的速度移动，经过多长时间，四边形BPDQ为菱形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示，对称轴为直线.下列结论中，正确的是（　　）

    A. abc>0 B. a+b=0 C. 2b+c>0 D. 4a+c<2b

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，自正方形ABCD的顶点A引两条射线分别交BC、CD于E、F，∠EAF=45°，在保持∠EAF=45°的前提下，当点E、F分别在边BC、CD上移动时，BE+DF与EF的关系是______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】综合与探究

    数学课上，老师让同学们利用三角形纸片进行操作活动，探究有关线段之间的关系.

    问题情境：

    如图1，三角形纸片ABC中，∠ACB＝90°，AC＝BC.将点C放在直线l上，点A，B位于直线l的同侧，过点A作AD⊥l于点D.

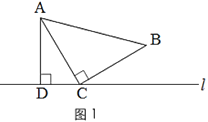
    初步探究：

    (1)在图1的直线l上取点E，使BE＝BC，得到图2.猜想线段CE与AD的数量关系，并说明理由；

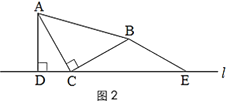
    变式拓展：

    (2)小颖又拿了一张三角形纸片MPN继续进行拼图操作，其中∠MPN＝90°，MP＝NP.小颖在图 1 的基础上，将三角形纸片MPN的顶点P放在直线l上，点M与点B重合，过点N作NH⊥l于点 H.

    请从下面 A，B 两题中任选一题作答，我选择_____题.

    A.如图3，当点N与点M在直线l的异侧时，探究此时线段CP，AD，NH之间的数量关系，并说明理由.

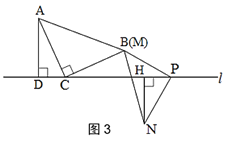
    B.如图4，当点N与点M在直线l的同侧，且点P在线段CD的中点时，探究此时线段CD，AD，NH之间的数量关系，并说明理由.

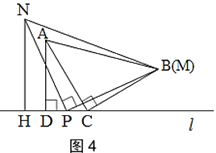
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线AB、CD相交于点O,∠AOC=30°，半径为1cm的⊙P的圆心在射线OA上，开始时，PO=6cm，如果⊙P以1cm/秒的速度沿由A向B的方向移动，那么当⊙P的运动时间t（秒）满足什么条件时，⊙P与直线CD相交?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若一次函数y=kx+b的自变量x的取值范围是-2≤x≤6，相应的函数值的范围是-11≤y≤9，求此函数的表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点．
    （1）在图1中以格点为顶点画一个面积为10的正方形；
    （2）在图2中以格点为顶点画一个三角形，使三角形三边长分别为2、、；
    （3）如图3，点A、B、C是小正方形的顶点，求∠ABC的度数．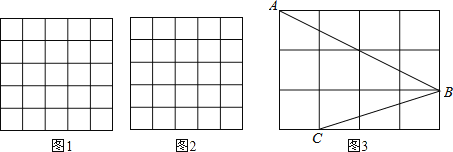

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了保护环境，某开发区综合治理指挥部决定购买A，B两种型号的污水处理设备共10台．已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同，每台设备价格及月处理污水量如下表所示：

    （1）求m的值；

    （2）由于受资金限制，指挥部用于购买污水处理设备的资金不超过165万元，问采用何种购买方案可以使得每月处理污水量的吨数为最多？并求出最多吨数．

    查看答案和解析>>

    同步练习册答案