
【题目】如图,![]() 是矩形
是矩形![]() 内一点,
内一点,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() .
.

![]() 请判断四边形
请判断四边形![]() 是否是正方形?若是,写出证明过程:若不是,说明理由;
是否是正方形?若是,写出证明过程:若不是,说明理由;
![]() 延长
延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() ,求
,求![]() 的度数.
的度数.
【答案】![]() 四边形
四边形![]() 为正方形,理由见解析;(2)
为正方形,理由见解析;(2)![]()
【解析】
(1)由四边形ABCD为矩形可得∠ABC=90°,易得∠ABP+∠PBC=90°,由AP⊥BP,可得∠ABP+∠PAB=90°,易得∠PBC=∠PAB,由AAS定理可得△ABP≌△BCE,由全等三角形的性质可得AB=BC,易得结论;
(2)连接AC,由△ABP≌△BCE易得AP=BE,又CF=BE,可得AP=CF,易得四边形ACGP是平行四边形,可得∠ACB=∠BGC,由四边形ABCD是正方形,AC是对角线,可得∠ACB=∠BGP=45°.
解:![]() 四边形
四边形![]() 为正方形.
为正方形.
∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,
即![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中,
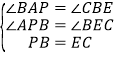 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∴矩形![]() 为正方形;
为正方形;
![]() 连接
连接![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∴![]() ,
,
∵四边形![]() 是正方形,
是正方形,![]() 是对角线,
是对角线,
∴![]() ,
,
∴![]() .
.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其顶点为D.

(1)抛物线及直线AC的函数关系式;
(2)设点M(3,m),求使MN+MD的值最小时m的值;
(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;
(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若△ABC内一点P,满足∠PAB=∠PBC=∠PCA=α,则称点P为△ABC的布洛卡点.通过研究一些特殊三角形中的布洛卡点,得到如下两个结论:
①若∠BAC=90°,则必有∠APC=90°;②若AB=AC,则必有∠APB=∠BPC.
对于这两个结论,下列说法正确的是( )
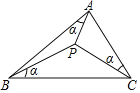
A.①对,②错B.①错,②对C.①,②均错D.①,②均对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB,AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为_____.
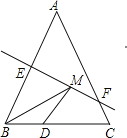
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,Rt△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.

(1)求证:AP=AO;
(2)求证:PE⊥AO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某庄有甲、乙两家草莓采摘园的草莓销售价格相同,春节期间,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为![]() (千克),在甲园所需总费用为
(千克),在甲园所需总费用为![]() (元),在乙园所需总费用为
(元),在乙园所需总费用为![]() (元),
(元),![]() 、
、![]() 与
与![]() 之间的函数关系如图所示.
之间的函数关系如图所示.

(1)甲采摘园的门票是_____元,两个采摘园优惠前的草莓单价是每千克____元;
(2)当![]() 时,求
时,求![]() 与
与![]() 的函数表达式;
的函数表达式;
(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB∥DE,AC∥DF,AC=DF下列条件中,不能判断△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农贸市场拟建两间长方形储藏室,储藏室的一面靠墙(墙长30m),中间用一面墙隔开,如图所示,已知建筑材料可建墙的长度为42m,则这两间长方形储藏室的总占地面积的最大值为_______m2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com