
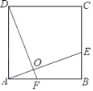
【题目】如图,在正方形ABCD中,AF=BE,AE与DF相交于于点O.
(1)求证:△DAF≌△ABE;
(2)求∠AOD的度数;
(3)若AO=4,DF=10,求![]() 的值.
的值.
【答案】(1)见解析;(2)![]() ;(3)tan∠ADF的值为
;(3)tan∠ADF的值为![]() .
.
【解析】
(1)利用正方形的性质得出AD=AB,∠DAB=∠ABC=90°,即可得出结论;
(2)利用(1)的结论得出∠ADF=∠BAE,进而求出∠ADF+∠DAO=90°,最后用三角形的内角和定理即可得出结论.
(3)根据(2)得到AO2=OF·OD,再设OF=x,DO=10-x,求出x即可解答
(1)在正方形ABCD中,DA=AB,![]() ,
,
又AF=BE
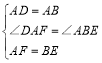
![]()
![]() ≌
≌![]() (SAS)
(SAS)
(2)由(1)得 ![]() ≌
≌![]() ,
,
![]()
![]() ADF=
ADF=![]() BAE,
BAE,
又 ![]() BAE+
BAE+![]() DAO=
DAO=![]() ,
,![]()
![]() ADF+
ADF+![]() DAO=
DAO=![]()
![]()
(3)由(2)得∠AOD=900 ∴△AOF∽△DOA ∴AO2=OF·OD
设OF=x,DO=10-x ∴x(10-x)=16 解得x=2或x=8(舍去)
∴tan∠ADF=![]()
∴tan∠ADF的值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8cm,BC=6cm,点P从点A出发,以lcm/s的速度沿A→D→C方向匀速运动,同时点Q从点A出发,以2cm/s的速度沿A→B→C方向匀速运动,当一个点到达点C时,另一个点也随之停止.设运动时间为t(s),△APQ的面积为S(cm2),下列能大致反映S与t之间函数关系的图象是( )
A.  B.
B. 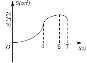 C.
C. 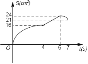 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
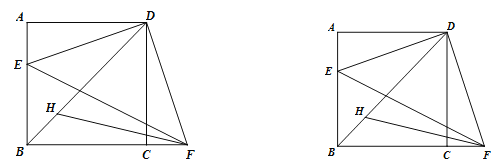
【题目】如图,在正方形ABCD中,E是边AB上的一动点,点F在边BC的延长线上,且![]() ,连接DE,DF,EF. FH平分
,连接DE,DF,EF. FH平分![]() 交BD于点H.
交BD于点H.
(1)求证:![]() ;
;
(2)求证:![]() :
:
(3)过点H作![]() 于点M,用等式表示线段AB,HM与EF之间的数量关系,并证明.
于点M,用等式表示线段AB,HM与EF之间的数量关系,并证明.
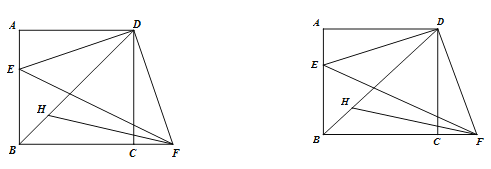
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1,在△ABC中,∠ACB=90°,BC=AC,点D在AB上,DE⊥AB交BC于E,点F是AE的中点
(1)写出线段FD与线段FC的关系并证明;
(2)如图2,将△BDE绕点B逆时针旋转α(0°<α<90°),其它条件不变,线段FD与线段FC的关系是否变化,写出你的结论并证明;
(3)将△BDE绕点B逆时针旋转一周,如果BC=4,BE=2![]() ,直接写出线段BF的范围.
,直接写出线段BF的范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区有一块长为30 m,宽为24 m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480 m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为________m.
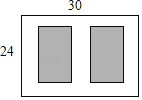
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加射击比赛,10次射击的成绩如表:
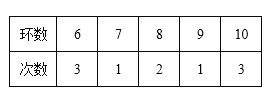
若小明再射击2次,分别命中7环、9环,与前10次相比,小明12次射击的成绩( )
A. 平均数变大,方差不变B. 平均数不变,方差不变
C. 平均数不变,方差变大D. 平均数不变,方差变小
查看答案和解析>>
科目:初中数学 来源: 题型:
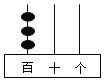
【题目】把3颗算珠放在计数器的3根插棒上构成一个数字,例如,如图摆放的算珠表示数300.现将3颗算珠任意摆放在这3根插棒上.
(1)若构成的数是两位数,则十位数字为1的概率为 ;
(2)求构成的数是三位数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境) 已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
(数学模型)
设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(![]() )(x>0)
)(x>0)
(探索研究)
我们可以借鉴以前研究函数的经验,先探索函数y=![]() (x>0)的图象和性质.
(x>0)的图象和性质.
(1)①填写下表,画出函数的图象;

②观察图象,写出该函数两条不同类型的性质;
③在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.请你通过配方求函数y=![]() (x>0)的最小值.
(x>0)的最小值.
解决问题:(2)用上述方法解决“问题情境”中的问题,直接写出答案。
查看答案和解析>>
科目:初中数学 来源: 题型:
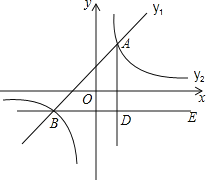
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() 和
和![]() .
.
![]() 求一次函数和反比例函数的表达式;
求一次函数和反比例函数的表达式;
![]() 请直接写出
请直接写出![]() 时,x的取值范围;
时,x的取值范围;
![]() 过点B作
过点B作![]() 轴,
轴,![]() 于点D,点C是直线BE上一点,若
于点D,点C是直线BE上一点,若![]() ,求点C的坐标.
,求点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com