
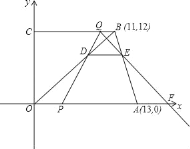
【题目】如图,在直角梯形OABC中,OA∥BC,A、B两点的坐标分别为A(13,0),B(11,12).动点P、Q分别从O、B两点出发,点P以每秒2个单位的速度沿x轴向终点A运动,点Q以每秒1个单位的速度沿BC方向运动;当点P停止运动时,点Q也同时停止运动.线段PQ和OB相交于点D,过点D作DE∥x轴,交AB于点E,射线QE交x轴于点F.设动点P、Q运动时间为t(单位:秒).
(1)当t为何值时,四边形PABQ是平行四边形.
(2)△PQF的面积是否发生变化?若变化,请求出△PQF的面积s关于时间t的函数关系式;若不变,请求出△PQF的面积.
(3)随着P、Q两点的运动,△PQF的形状也随之发生了变化,试问何时会出现等腰△PQF?
【答案】(1)t=![]() ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.
【解析】
(1)设OP=2t,QB=t,PA=13﹣2t,根据平行四边形的性质(对边平行且相等)知,只需QB=PA,从而求得t;
(2)根据平行线分线段成比例求得![]() =
=![]() ;然后由平行线OB∥DE∥PA分线段成比例求得
;然后由平行线OB∥DE∥PA分线段成比例求得![]() ;利用等量代换求得AF=2QB=2t,PF=OA=13;最后由三角形的面积公式求得△PQF的面积;
;利用等量代换求得AF=2QB=2t,PF=OA=13;最后由三角形的面积公式求得△PQF的面积;
(3)由(2)知,PF=OA=13.分三种情况解答:①QP=FQ,作QG⊥x轴于G,则11﹣t﹣2t=2t+13﹣(11﹣t);②PQ=FP;③FQ=FP.
解:(1)设OP=2t,QB=t,PA=13﹣2t,要使四边形PABQ为平行四边形,则13﹣2t=t
∴![]() .
.
(2)不变.
∵![]() ,
,
∴![]() ,
,
∵QB∥DE∥PA,
∴![]() ,
,
∴AF=2QB=2t,
∴PF=OA=13,
∴S△PQF=![]() ;
;
(3)由(2)知,PF=OA=13,
①QP=FQ,作QG⊥x轴于G,则11﹣t﹣2t=2t+13﹣(11﹣t),
∴t=![]() ;
;
②PQ=FP,
∴![]() ,
,
∴t=2或![]() ;
;
③FQ=FP,
∴![]() ,
,
∴t=1;
综上,当t=![]() 或1或2或
或1或2或![]() 时,△PQF是等腰三角形.
时,△PQF是等腰三角形.


科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点A,B,与
与x轴交于点A,B,与![]() 轴交于点C。过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD。已知点A坐标为(-1,0)。
轴交于点C。过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD。已知点A坐标为(-1,0)。

(1)求该抛物线的解析式;
(2)求梯形COBD的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
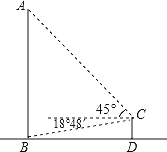
【题目】全球最大的关公塑像矗立在荆州古城东门外.如图,张三同学在东门城墙上C处测得塑像底部B处的俯角为18°48′,测得塑像顶部A处的仰角为45°,点D在观测点C正下方城墙底的地面上,若CD=10米,则此塑像的高AB约为 米(参考数据:tan78°12′≈4.8).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 O 是△ABC 的边 AB 上一点,以 OB 为半径的⊙O 交 BC 于点 D,过点 D 的切线交 AC 于点 E,且 DE⊥AC.
(1)证明:AB=AC;
(2)设 AB=![]() cm,BC=2cm,当点 O 在 AB 上移动到使⊙O 与边 AC 所在直线相切时, 求⊙O 的半径.
cm,BC=2cm,当点 O 在 AB 上移动到使⊙O 与边 AC 所在直线相切时, 求⊙O 的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C、D均在⊙O上,FB与⊙O相切于点B,AB与CF交于点G,OA⊥CF于点E,AC∥BF.
(1)求证:FG=FB.
(2)若tan∠F=![]() ,⊙O的半径为4,求CD的长.
,⊙O的半径为4,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,则下列结论中:①ac>0;②a+b+c<0;③4a﹣2b+c<0;④2a+b<0;⑤4ac﹣b2<4a;⑥a+b>0中,其中正确的个数为( )
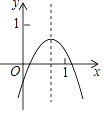
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高![]() 米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心
米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心![]() 米.
米.

(1)请你建立适当的直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
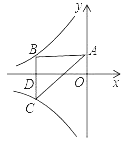
【题目】如图所示双曲线y=![]() 与y=﹣
与y=﹣![]() 分别位于第三象限和第二象限,A是y轴上任意一点,B是y=﹣
分别位于第三象限和第二象限,A是y轴上任意一点,B是y=﹣![]() 上的点,C是y=
上的点,C是y=![]() 上的点,线段BC⊥x轴于D,且4BD=3CD,则下列说法:①双曲线y=
上的点,线段BC⊥x轴于D,且4BD=3CD,则下列说法:①双曲线y=![]() 在每个象限内,y随x的增大而减小;②若点B的横坐标为﹣3,则C点的坐标为(﹣3,
在每个象限内,y随x的增大而减小;②若点B的横坐标为﹣3,则C点的坐标为(﹣3,![]() );③k=4;④△ABC的面积为定值7,正确的有( )
);③k=4;④△ABC的面积为定值7,正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
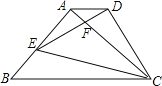
【题目】如图,△ABC为等腰直角三角形,∠BAC=90°,BC=1,E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连结AD,下列说法:①∠BCE=∠ACD;②△ACD∽△BCE;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为![]() .其中正确的结论是_________.
.其中正确的结论是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com