
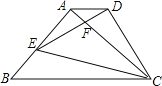
【题目】如图,△ABC为等腰直角三角形,∠BAC=90°,BC=1,E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连结AD,下列说法:①∠BCE=∠ACD;②△ACD∽△BCE;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为![]() .其中正确的结论是_________.
.其中正确的结论是_________.
【答案】①②④⑤
【解析】
①首先根据等腰三角形的性质得到∠ACB=∠DCE=45°,从而得到∠ACB﹣∠ACE=∠DCE﹣∠ACE,进而得到结论:∠ECB=∠DCA正确;②利用两组对应边成比例,夹角相等的三角形相似证得结论△ADC∽△BEC即可;④证得△ADC∽△BEC后得到∠DAC=∠B=45°,从而得到∠DAC=∠BCA=45°,即AD∥BC;③由④知:△EAD与△BEC不相似,故③错误;⑤△ABC的面积为定值,若梯形ABCD的面积最大,则△ACD的面积最大;△ACD中,AD边上的高为定值(即为1),若△ACD的面积最大,则AD的长最大;由④的△BEC∽△ADC知:当AD最长时,BE也最长;故梯形ABCD面积最大时,E、A重合,此时EC=AC=![]() ,AD=
,AD=![]() ,故S梯形ABCD=
,故S梯形ABCD=![]() (1+
(1+![]() )×
)×![]() =
=![]() ,从而判定是否正确即可;
,从而判定是否正确即可;
∵△ABC、△DCE都是等腰直角三角形,
∴AB=AC=![]() BC=
BC=![]() ,CD=DE=
,CD=DE=![]() CE;∠B=∠ACB=∠DEC=∠DCE=45°;
CE;∠B=∠ACB=∠DEC=∠DCE=45°;
①∵∠ACB=∠DCE=45°,
∴∠ACB﹣∠ACE=∠DCE﹣∠ACE;
即∠ECB=∠DCA;故①正确;
②![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ;
;
由①知∠ECB=∠DCA,
∴△BEC∽△ADC;故②正确;
④由②得△BEC∽△ADC,
∴∠DAC=∠B=45°;
∴∠DAC=∠BCA=45°,即AD∥BC,故④正确;
③由④知:∠DAC=45°,则∠EAD=135°;
∠BEC=∠EAC+∠ECA=90°+∠ECA;
∵∠ECA<45°,
∴∠BEC<135°,即∠BEC<∠EAD;
因此△EAD与△BEC不相似,故③错误;
⑤△ABC的面积为定值,若梯形ABCD的面积最大,则△ACD的面积最大;
△ACD中,AD边上的高为定值(即为1),若△ACD的面积最大,则AD的长最大;
由④的△BEC∽△ADC知:当AD最长时,BE也最长;
故梯形ABCD面积最大时,E、A重合,此时EC=AC=![]() ,AD=
,AD=![]() ;
;
故S梯形ABCD=![]() (1+
(1+![]() )×
)×![]() =
=![]() ,故⑤正确;
,故⑤正确;
故正确的结论是①②④⑤,
故答案为:①②④⑤


科目:初中数学 来源: 题型:
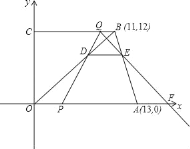
【题目】如图,在直角梯形OABC中,OA∥BC,A、B两点的坐标分别为A(13,0),B(11,12).动点P、Q分别从O、B两点出发,点P以每秒2个单位的速度沿x轴向终点A运动,点Q以每秒1个单位的速度沿BC方向运动;当点P停止运动时,点Q也同时停止运动.线段PQ和OB相交于点D,过点D作DE∥x轴,交AB于点E,射线QE交x轴于点F.设动点P、Q运动时间为t(单位:秒).
(1)当t为何值时,四边形PABQ是平行四边形.
(2)△PQF的面积是否发生变化?若变化,请求出△PQF的面积s关于时间t的函数关系式;若不变,请求出△PQF的面积.
(3)随着P、Q两点的运动,△PQF的形状也随之发生了变化,试问何时会出现等腰△PQF?
查看答案和解析>>
科目:初中数学 来源: 题型:
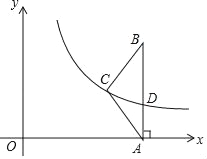
【题目】如图,在△ABC中,AC=BC=5,AB=8,AB⊥x轴,垂足为A,反比例函数y=![]() (x>0)的图象经过点C,交AB于点D.
(x>0)的图象经过点C,交AB于点D.
(1)若OA=AB,求k的值;
(2)若BC=BD,连接OC,求△OAC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
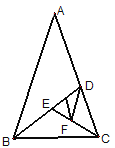
【题目】如图,顶角为36°的等腰三角形,其底边与腰之比等![]() ,这样的三角形称为黄金三角形,已知腰AB=1,△ABC为第一个黄金三角形,△BCD为第二个黄金三角形,△CDE为第三个黄金三角形,以此类推,第2014个黄金三角形的周长( )
,这样的三角形称为黄金三角形,已知腰AB=1,△ABC为第一个黄金三角形,△BCD为第二个黄金三角形,△CDE为第三个黄金三角形,以此类推,第2014个黄金三角形的周长( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB=1,点P1是线段AB的黄金分割点(且AP1<BP1,即P1B2=AP1AB),点P2是线段AP1的黄金分割点(AP2<P1P2),点P3是线段AP2的黄金分割点(AP3<P2P3),…,依此类推,则线段AP2017的长度是( )
![]()
A. (![]() )2017 B. (
)2017 B. (![]() )2017 C. (
)2017 C. (![]() )2017 D. (
)2017 D. (![]() ﹣2)1008
﹣2)1008
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】折纸与证明﹣﹣﹣用纸折出黄金分割点:
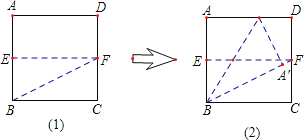
第一步:如图(1),先将一张正方形纸片ABCD对折,得到折痕EF;再折出矩形BCFE的对角线BF.
第二步:如图(2),将AB边折到BF上,得到折痕BG,试说明点G为线段AD的黄金分割点(AG>GD)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数![]() (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B(![]() ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C.

(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
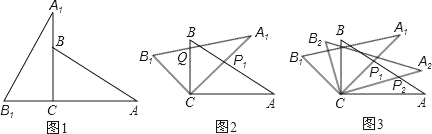
【题目】将两块全等的三角板如图1摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.
(1)将图1中△A1B1C绕点C顺时针旋转45°得图2,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;
(2)在图2中,若AP1=a,则CQ等于多少?
(3)将图2中△A1B1C绕点C顺时针旋转到△A2B2C(如图3),点P2是A2C与AP1的交点.当旋转角为多少度时,有△AP1C∽△CP1P2?这时线段CP1与P1P2之间存在一个怎样的数量关系?.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】几何体的三视图相互关联.已知直三棱柱的三视图如图,在△PMN中,∠MPN=90°,PN=4,sin∠PMN=![]() .
.
(1)求BC及FG的长;
(2)若主视图与左视图两矩形相似,求AB的长;
(3)在(2)的情况下,求直三棱柱的表面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com