

���� ��1����ͼ1���������ε����ʾͿ��Եó�AO=BO=CO=DO=5����AOB=��BOC=90�㣮��ACB=��BAC=45�㣬��ƽ���ߵ����ʾͿ������PM��ֵ���ɵ��������ε����ʾͿ������PN��ֵ��
��2����ͼ2���ӳ�NP��AD��G���Ϳ��Եó��ı���GNBD��ƽ���ı��Σ�����NG=BD����֤��PM=PG�Ϳ��Եó����ۣ�
��3����BG��MN��G�������ε����ʾͿ��Եó�BM=BN�����ݵ��������ε����ʾͿ��Եó�MG=NG���Ӷ��ó��ı���BGPOΪ���Σ��ɾ��ε����ʾͿ��Եó����ۣ�
��� �⣺��1����ͼ1�����ı���ABCD�������Σ�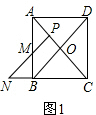
��AO=BO=CO=DO����AOB=��BOC=90�㣮��ACB=��BAC=45�㣮
��PM��OB��
���AMP�ס�ABO����NPC=��BOC=90�㣬
���N=45�㣬
���N=��ACB��
��PN=PC��
��$\frac{AP}{AO}=\frac{MP}{BO}$��
��AP=3��OB=5��
��AO=5��PO=2��
��PC=7��
��PN=7
��$\frac{3}{5}=\frac{PM}{5}$��
��PM=3��
�ʴ�Ϊ��3��7��
��2��PM+PN=2OB��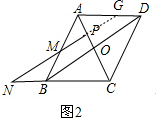
���ɣ���ͼ2�����ı���ABCD�����Σ�
��AD��BC����BAC=��DAC����AOB=��AOD=90�㣬BD=2BO��
��PM��OB��
���APM=��APG=90�㣮
�ڡ�APM�͡�APG�У�
$\left\{\begin{array}{l}{��BAC=��DAC}\\{AP=AP}\\{��APM=��APG}\end{array}\right.$��
���APM�ա�APG��ASA����
��PM=PG��
��PM+PN=PG+PN=NG��
��PN��BO��AD��BC��
���ı���NBDG��ƽ���ı��Σ�
��NG=BD��
��NG=2BO��
��PM+PN=2BO��
��3��PM-PN=2BO��
���ɣ���ͼ3�����ı���ABCD�����Σ�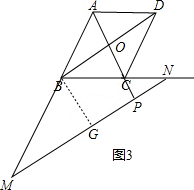
��AD��BC����ABD=��CBD����AOB=��AOD=��POB=90�㣬BD=2BO��
��PM��OB��
���APM=��APG=90�㣮��CBD=��BNP����ADB=��M��
���BNP=��M��
��BM=BN��
��BG��MN��G��
���BGP=90�㣬MG=NG��
���POB=��APG=��BGP=90�㣬
���ı���BGPO�Ǿ��Σ�
��GP=BO��
��GP=GN-PN��
��OB+GP=MG-PN+GP��
��0B+OB=MP-PN��
��MP-PN=2OB��
���� ���⿼���������ε����ʵ����ã�ƽ���ߵ����ʵ����ã����������ε��ж������ʵ����ã�ƽ���ı��ε��ж������ʵ����ã����ε��ж������ʵ����ã����������ε����ʵ����ã����ʱ����ƽ���ı��ε���������ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
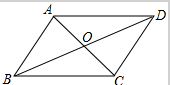 ��ͼ��ƽ���ı���ABCD�������Խ����ཻ��O������COD�����Ϊ6�����ABD�����12��
��ͼ��ƽ���ı���ABCD�������Խ����ཻ��O������COD�����Ϊ6�����ABD�����12���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
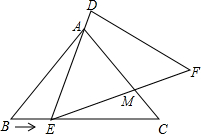 ��ͼ���ڡ�ABC�У���֪AB=AC=5��BC=6���ҡ�ABC�ա�DEF������DEF���ABC�غ���һ�𣬡�ABC��������ABC��������DEF�˶��������㣺��E�ڱ�BC����B��C�ķ����˶���E����B��C�غϣ�����DEʼ�վ�����A��EF��AC����M�㣮
��ͼ���ڡ�ABC�У���֪AB=AC=5��BC=6���ҡ�ABC�ա�DEF������DEF���ABC�غ���һ�𣬡�ABC��������ABC��������DEF�˶��������㣺��E�ڱ�BC����B��C�ķ����˶���E����B��C�غϣ�����DEʼ�վ�����A��EF��AC����M�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com