
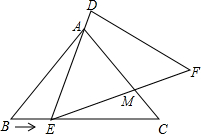
 如图,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动(E不与B、C重合),且DE始终经过点A,EF与AC交于M点.
如图,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动(E不与B、C重合),且DE始终经过点A,EF与AC交于M点.分析 (1)由AB=AC,根据等边对等角,可得∠B=∠C,又由△ABC≌△DEF与三角形外角的性质,易证出∠CEM=∠BAE,从而可证得△ABE∽△ECM;
(2)首先由∠AEF=∠B=∠C,且∠AME>∠C,可得AE≠AM,然后分别从AE=EM与AM=EM去分析,注意利用全等三角形与相似三角形的性质求解即可求得答案.
解答 (1)证明:∵AB=AC,
∴∠B=∠C,
∵△ABC≌△DEF,
∴∠AEF=∠B,
又∵∠AEF+∠CEM=∠AEC=∠B+∠BAE,
∴∠CEM=∠BAE,
∴△ABE∽△ECM;
(2)能.
解:∵∠AEF=∠B=∠C,且∠AME>∠C,
∴∠AME>∠AEF,
∴AE≠AM;
当AE=EM时,则△ABE≌△ECM,
∴CE=AB=5,
∴BE=BC-EC=6-5=1,
当AM=EM时,则∠MAE=∠MEA,
∴∠MAE+∠BAE=∠MEA+∠CEM,
即∠CAB=∠CEA,
又∵∠C=∠C,
∴△CAE∽△CBA,
∴$\frac{CE}{AC}$=$\frac{AC}{CB}$,
∴CE=$\frac{A{C}^{2}}{CB}$,
∴BE=6-$\frac{25}{6}$=$\frac{11}{6}$;
∴BE=1或$\frac{11}{6}$.
点评 此题考查了相似形综合,用到的知识点是相似三角形的判定与性质、全等三角形的判定与性质,此题难度较大,注意数形结合思想、分类讨论思想与函数思想的应用是解此题的关键.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
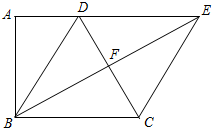 如图,在梯形ABCD中,AD∥BC,∠A=∠ABC=90°,且AD=$\frac{1}{2}$CD.将梯形ABCD沿对角线BD折叠,点A恰好落在CD边的点F上,延长BF交AD延长线于点E,连接EC.
如图,在梯形ABCD中,AD∥BC,∠A=∠ABC=90°,且AD=$\frac{1}{2}$CD.将梯形ABCD沿对角线BD折叠,点A恰好落在CD边的点F上,延长BF交AD延长线于点E,连接EC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com