
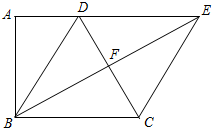
 如图,在梯形ABCD中,AD∥BC,∠A=∠ABC=90°,且AD=$\frac{1}{2}$CD.将梯形ABCD沿对角线BD折叠,点A恰好落在CD边的点F上,延长BF交AD延长线于点E,连接EC.
如图,在梯形ABCD中,AD∥BC,∠A=∠ABC=90°,且AD=$\frac{1}{2}$CD.将梯形ABCD沿对角线BD折叠,点A恰好落在CD边的点F上,延长BF交AD延长线于点E,连接EC.分析 (1)利用折叠和AD=$\frac{1}{2}$CD,得出DF=CF,利用ASA得出△DEF≌△CBF;
(2)先利用DF=FC,EF=BF,得出四边形BCED是平行四边形,再进一步证明△DBF≌△CFE,得出DB=DE,证得四边形BCED是菱形;
(3)利用折叠得出∠ADB=∠CDB,利用菱形得出∠CDB=∠CDE,由此得出∠ADB=∠CDB=∠CDE=60°,得出∠ADC=120°.
解答 (1)证明:∵梯形ABCD沿对角线BD折叠,点A恰好落在CD边的点F上,
∴∠DFB=∠A=90°,AD=DF,
∵AD=$\frac{1}{2}$CD,
∴DF=$\frac{1}{2}$CD,
∴DF=CF,
∵AD∥BC,
∴∠FDE=∠FCB,
在△DEF和△CBF中,
$\left\{\begin{array}{l}{∠FDE=∠FCB}\\{DF=CF}\\{∠DFE=∠CFB}\end{array}\right.$
∴△DEF≌△CBF;
(2)四边形BCED是菱形.
理由:∵△DEF≌△CBF,
∴DF=FC,EF=BF,
∴四边形BCED平行四边形,
在△DBF和△CFE中,
$\left\{\begin{array}{l}{BF=EF}\\{∠DFB=∠DFE}\\{DF=DF}\end{array}\right.$
∴△DBF≌△CFE,
∴DB=DE,
∴四边形BCED是菱形.
(3)∠ADC=120°.
∵折叠,
∴∠ADB=∠CDB,
∵四边形BCED是菱形,
∴∠CDB=∠CDE,
∴∠ADB=∠CDB=∠CDE=60°,
∴∠ADC=120°.
点评 此题综合考查三角形全等的判定与性质,折叠的性质,菱形的判定,注意已知条件与所求问题之间的联系,灵活运用知识之间的联系解决问题.


科目:初中数学 来源: 题型:解答题
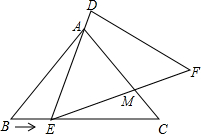 如图,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动(E不与B、C重合),且DE始终经过点A,EF与AC交于M点.
如图,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动(E不与B、C重合),且DE始终经过点A,EF与AC交于M点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
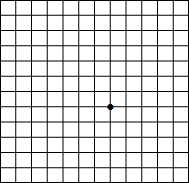 如图,这是我军缴获的敌人埋设地雷的地图.通过破译的密码知道,一棵大树作为参照物,树的坐标是(10,-10).这个区域埋设地雷的坐标分别是(10,20),(0,50),(-50,-40),(-40,40),(50,-30),(-10,0).
如图,这是我军缴获的敌人埋设地雷的地图.通过破译的密码知道,一棵大树作为参照物,树的坐标是(10,-10).这个区域埋设地雷的坐标分别是(10,20),(0,50),(-50,-40),(-40,40),(50,-30),(-10,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
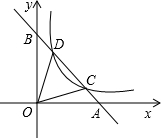 如图,直线AB过点A(8,0)、B(0,6).反比例函数$y=\frac{p}{x}$(p>0)的图象与直线AB交于C、D两点,连接OC、OD.
如图,直线AB过点A(8,0)、B(0,6).反比例函数$y=\frac{p}{x}$(p>0)的图象与直线AB交于C、D两点,连接OC、OD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com