
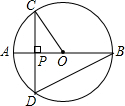
 已知AB是⊙O的直径,弦CD⊥AB,垂足为P,
已知AB是⊙O的直径,弦CD⊥AB,垂足为P,分析 (1)由直径AB垂直于弦CD,利用垂径定理得到P为CD的中点,由CD的长求出CP的长,再由圆的半径OC的长,在直角三角形CPO中,利用勾股定理求出OP的长,再在直角三角形BDP中得出BD的长;
(2)根据圆周角定理和∠AOC=40°,即可得出∠B的度数.
解答 解:(1)∵AB是⊙O的直径,弦CD⊥AB,
∴CP=DP,
∵CD=8,
∴CP=4,
∵OC=5,
∵OP2+CP2=OC2,
∴OP=3,
∴BP=8,
∵DP2+BP2=BD2,
∴BD=4$\sqrt{5}$;
(2)∵AB是⊙O的直径,弦CD⊥AB,
∴$\widehat{AC}$=$\widehat{AD}$,
∴∠B=$\frac{1}{2}$∠AOC,
∵∠AOC=40°,
∴∠B=20°.
点评 本题考查了垂径定理,以及勾股定理,垂径定理的内容为:垂直于弦的直径平分于弦,且平分弦所对的弧,熟练掌握定理是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
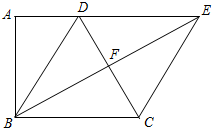 如图,在梯形ABCD中,AD∥BC,∠A=∠ABC=90°,且AD=$\frac{1}{2}$CD.将梯形ABCD沿对角线BD折叠,点A恰好落在CD边的点F上,延长BF交AD延长线于点E,连接EC.
如图,在梯形ABCD中,AD∥BC,∠A=∠ABC=90°,且AD=$\frac{1}{2}$CD.将梯形ABCD沿对角线BD折叠,点A恰好落在CD边的点F上,延长BF交AD延长线于点E,连接EC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
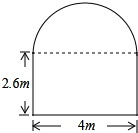 如图所示,某住宅社区在相邻两楼之间修建一个上方是一个半圆,下方是长方形的仿古通道,现有一辆卡车装满家具后,高4米,宽2.4米,请问这辆送家具的卡车能否通过这个通道?
如图所示,某住宅社区在相邻两楼之间修建一个上方是一个半圆,下方是长方形的仿古通道,现有一辆卡车装满家具后,高4米,宽2.4米,请问这辆送家具的卡车能否通过这个通道?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
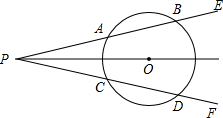 如图所示,点O是∠EPF平分线上的一点,以点O为圆心的圆与角的两边分别交于点A、B和C、D.
如图所示,点O是∠EPF平分线上的一点,以点O为圆心的圆与角的两边分别交于点A、B和C、D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
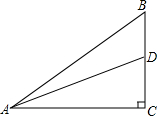 如图,在Rt△ABC中,AB=15,Sin∠BAC=$\frac{3}{5}$,点D是BC边上一点,且BD=4,求:(1)线段AC的长;(2)tan∠ADC的值.
如图,在Rt△ABC中,AB=15,Sin∠BAC=$\frac{3}{5}$,点D是BC边上一点,且BD=4,求:(1)线段AC的长;(2)tan∠ADC的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com