
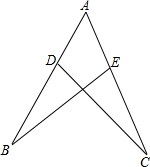
 已知:AD=AE,∠B=∠C,证明:AC=AB.
已知:AD=AE,∠B=∠C,证明:AC=AB.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,这是我军缴获的敌人埋设地雷的地图.通过破译的密码知道,一棵大树作为参照物,树的坐标是(10,-10).这个区域埋设地雷的坐标分别是(10,20),(0,50),(-50,-40),(-40,40),(50,-30),(-10,0).
如图,这是我军缴获的敌人埋设地雷的地图.通过破译的密码知道,一棵大树作为参照物,树的坐标是(10,-10).这个区域埋设地雷的坐标分别是(10,20),(0,50),(-50,-40),(-40,40),(50,-30),(-10,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
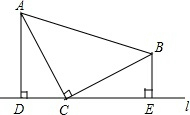 已知:如图,等腰三角形ABC中,AC=BC,∠ACB=90°,直线l经过点C(点A、B都在直线l的同侧),AD⊥l,BE⊥l,垂足分别为D、E.
已知:如图,等腰三角形ABC中,AC=BC,∠ACB=90°,直线l经过点C(点A、B都在直线l的同侧),AD⊥l,BE⊥l,垂足分别为D、E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
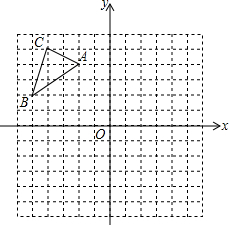 已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移4个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度)
已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移4个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com