【题目】为了倡导“节约用水，从我做起”，市政府决定对市直机关500户家庭的用水情况作一次调查，市政府调查小组随机抽查了其中100户家庭一年的月平均用水量（单位：吨）．并将调查结果绘制成了如图所示的条形统计图，则这组数据的众数和中位数分别是（ ）
A.40，20
B.11，11
C.11，12
D.11，11.5
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，E是AD边的中点，BE⊥AC，垂足为点F，连接DF，分析下列四个结论：
①△AEF∽△CAB；②CF=2AF；③DF=DC；④tan∠CAD= 
．
其中正确的结论有（ ）
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线l1：y1＝﹣
x+b分别与x轴、y轴交于点A、点B，与直线l2：y2＝x交于点C（2，2）．
（1）若y1＜y2，请直接写出x的取值范围；
（2）点P在直线l1：y1＝﹣x+b上，且△OPC的面积为3，求点P的坐标？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，要得到AB∥CD，只需要添加一个条件，这个条件不可以是（ ）
A. ∠1＝∠3 B. ∠B＋∠BCD＝180°
C. ∠2＝∠4 D. ∠D＋∠BAD＝180°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲乙两同学用一副扑克牌中牌面数字分别是3，4，5，6的4张牌做抽数字游戏，游戏规则是：将这4张牌的正面全部朝下，洗匀，从中随机抽取一张，抽得的数作为十位上的数字，抽出的牌不放回，然后将剩下的牌洗匀，再从中随机抽取一张，抽得的数作为个位上的数字，这样就得到一个两位数，若这个两位数小于45，则甲获胜，否则乙获胜．你认为这个游戏公平吗？请利用树状图或列表法说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读材料并完成任务．
莱昂哈德·欧拉是18世纪数学界最杰出的人物之一，瑞士著名的数学家、物理学家，他不但为数学界作出贡献，更把整个数学推至物理的领域；同时，也是数学史上研究成果最多的数学家，平均每年写出八百多页的论文，还写了大量的力学、分析学、几何学等的课本，《无穷小分析引论》《微分学原理》《积分学原理》等都成为数学界中的经典著作．因此，被称为历史上最伟大的两位数学家之一（另一位是卡尔·弗里德里克·高斯）．在数学成就上，欧拉最先把关于
的多项式用记号
的形式来表示（
可用其他字母代替，但不同的字母表示不同的多项式），例如
，当
时，多项式的值用
来表示，即
；当
时，多项式的值用
来表示，记为
．
任务：
已知
；
．
请你根据材料中代入求值的方法解决下列问题：
（1）求
的值；
（2）求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
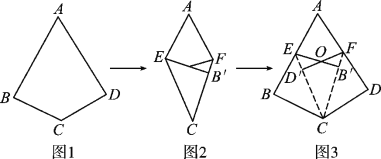
【题目】阅读理解：如图1，如果四边形ABCD满足AB＝AD，CB＝CD，∠B＝∠D＝90°，那么我们把这样的四边形叫做“完美筝形”．将一张如图1所示的“完美筝形”纸片ABCD先折叠成如图2所示形状，再展开得到图3，其中CE，CF为折痕，∠BCE＝∠ECF＝∠FCD，点B′为点B的对应点，点D′为点D的对应点，连接EB′，FD′相交于点O.
简单应用：
(1)在平行四边形、矩形、菱形、正方形四种图形中，一定为“完美筝形”的是 ；
(2)当图3中的∠BCD＝120°时，∠AEB′＝ ；
拓展提升：
(3)当图2中的四边形AECF为菱形时，对应图3中的四边形CD′OB′是否是“完美筝形”？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC内接于⊙O，且∠B=60°，过C作⊙O的切线l，与直径AD的延长线交于点E，AF⊥l，垂足为F．
（1）求证：AC平分∠FAD；
（2）已知AF=3 
，求阴影部分面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，AB为⊙O的直径，PD切⊙O于点C，与BA的延长线交于点D，DE⊥PO交PO延长线于点E，连接PB，∠EDB=∠EPB．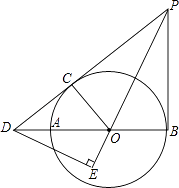
（1）求证：PB是⊙O的切线；
（2）若PB=9，DB=12，求⊙O的半径．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
