
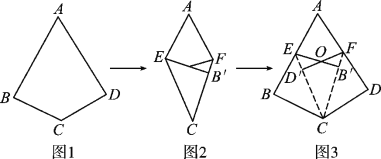
【题目】阅读理解:如图1,如果四边形ABCD满足AB=AD,CB=CD,∠B=∠D=90°,那么我们把这样的四边形叫做“完美筝形”.将一张如图1所示的“完美筝形”纸片ABCD先折叠成如图2所示形状,再展开得到图3,其中CE,CF为折痕,∠BCE=∠ECF=∠FCD,点B′为点B的对应点,点D′为点D的对应点,连接EB′,FD′相交于点O.
简单应用:
(1)在平行四边形、矩形、菱形、正方形四种图形中,一定为“完美筝形”的是 ;
(2)当图3中的∠BCD=120°时,∠AEB′= ;
拓展提升:
(3)当图2中的四边形AECF为菱形时,对应图3中的四边形CD′OB′是否是“完美筝形”?请说明理由.
【答案】(1)正方形;(2)80°;(3)四边形CD′OB′是“完美筝形”,理由详见解析.
【解析】
(1)根据“完美风筝”的定义判断即可得到结果;
(2)根据根据∠BCE=∠ECF=∠FCD,可得到∠BCE=![]() ∠BCD=40°,由三角形的内角和可得∠BEC=50°,根据对折得到∠BEC=∠B′EC,根据邻补角即可求解;
∠BCD=40°,由三角形的内角和可得∠BEC=50°,根据对折得到∠BEC=∠B′EC,根据邻补角即可求解;
(3)根据“完美筝形”的定义得出线段、角相等,转化到四边形ODCB中,即可.
解:(1)∵若四边形ABCD是正方形,
∴AB=AD,CB=CD,∠B=∠D=90°,
∴正边形一定是“完美筝形”
(2)由对折有,∠BEC=∠B′EC,
∵∠BCE=∠ECF=∠FCD,且∠BCD=120°,
∴∠BCE=![]() ∠BCD=40°,
∠BCD=40°,
∴∠BEC=90°﹣∠BCE=50°,
∴∠BEB′=100°
∴∠AEB′=80°,
(3)四边形CD′OB′是“完美筝形”.
理由:∵四边形ABCD是“完美筝形”,
∴CB=CD,∠B=∠D=90°.
由折叠可知,CD′=CD,CB′=CD,∠CD′O=∠CB′O=90°,
∴CD′=CB′,∠OD′E=∠OB′F=90°.
∵四边形AECF为菱形,
∴CE=CF,
∴D′E=B′F,
在△OED′和△OFB′中,
∴△OED′≌△OFB′(AAS),
∴OD′=OB′,
∴四边形CD′OB′是“完美筝形”.
故答案为:(1)正方形;(2)80°;(3)四边形CD′OB′是“完美筝形”,理由详见解析.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,C是线段AB上一点,M是线段AC的中点,N是线段BC的中点.
(1)如果AB=20 cm,AM=6 cm,求NC的长;
(2)如果MN=6 cm,求AB的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
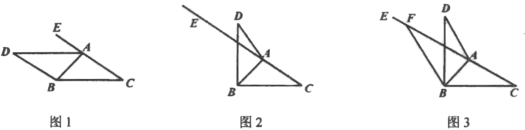
【题目】如图,在![]() 的
的![]() 边的异侧作
边的异侧作![]() ,并使
,并使![]() .点
.点![]() 在射线
在射线![]() 上.
上.
(1)如图,若![]() ,求证:
,求证:![]() ;
;
(2)若![]() ,试解决下面两个问题:
,试解决下面两个问题:
①如图2,![]() ,求
,求![]() 的度数;
的度数;
②如图3,若![]() ,过点
,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,当
,当![]() 时,求
时,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了倡导“节约用水,从我做起”,市政府决定对市直机关500户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨).并将调查结果绘制成了如图所示的条形统计图,则这组数据的众数和中位数分别是( )
A.40,20
B.11,11
C.11,12
D.11,11.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
阅读理解:数轴是学习有理数的一种重要工具,任何有理数都可以用数轴上的点表示,这样能够运用数形结合的方法解决一些问题.例如,两个有理数在数轴上对应的点之间的距离可以用较大数与较小数的差来表示.例如:
在数轴上,有理数3与1对应的两点之间的距离为![]() ;
;
在数轴上,有理数3与-2对应的两点之间的距离为![]() ;
;
在数轴上,有理数-3与-2对应的两点之间的距离为![]() .
.
解决问题:如图所示,已知点![]() 表示的数为-3,点
表示的数为-3,点![]() 表示的数为-1,点
表示的数为-1,点![]() 表示的数为2.
表示的数为2.
![]()
(1)点![]() 和点
和点![]() 之间的距离为______.
之间的距离为______.
(2)若数轴上动点![]() 表示的数为
表示的数为![]() ,当
,当![]() 时,点
时,点![]() 和点
和点![]() 之间的距离可表示为______;当
之间的距离可表示为______;当![]() 时,点
时,点![]() 和点
和点![]() 之间的距离可表示为______.
之间的距离可表示为______.
(3)若数轴上动点![]() 表示的数为
表示的数为![]() ,点
,点![]() 在点
在点![]() 和点
和点![]() 之间,点
之间,点![]() 和点
和点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 和点
和点![]() 之间的距离表示为
之间的距离表示为![]() ,求
,求![]() (用含
(用含![]() 的代数式表示并进行化简)
的代数式表示并进行化简)
(4)若数轴上动点![]() 表示的数为-2,将点
表示的数为-2,将点![]() 向右移动19个单位长度,再向左移动23个单位长度终点为
向右移动19个单位长度,再向左移动23个单位长度终点为![]() ,那么
,那么![]() ,
,![]() 两点之间的距离是______.
两点之间的距离是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若三角形的一边和该边上的高相等的三角形称为“和谐三角形”,如图,已知抛物线y=ax2经过A(﹣1,1),P是y轴正半轴上的动点,射线AP与抛物线交于另一点B,当△AOP是“和谐三角形”时,点B的坐标为 . 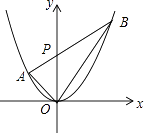
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知长方形纸片ABCD,点E在边AB上,点F、G在边CD上,连接EF、EG.将∠BEG对折,点B落在直线EG上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN.
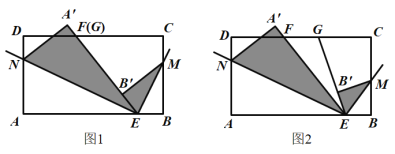
(1)如图1,若点F与点G重合,求∠MEN的度数;
(2)如图2,若点G在点F的右侧,且∠FEG=30°,求∠MEN的度数;
(3)若∠MEN=α,请直接用含α的式子表示∠FEG的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=80°,∠D=30°,求∠AEM的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com