
分析 (1)首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集;
(2)首先去分母,然后去括号、移项、合并同类项、系数化成1即可求解.
解答 解:(1)$\left\{\begin{array}{l}{5x-3<41…①}\\{4(x-1)+3≥2x…②}\end{array}\right.$,
解①得x<$\frac{44}{5}$,
解②得x≥$\frac{1}{2}$.
则不等式组的解集是$\frac{1}{2}$≤x<$\frac{44}{5}$;
(2)去分母,得3(3y-1)<10y+5-6,
去括号,得9y-3<10y+5-6,
移项,得9y-10y<5-6+3,
合并同类项,得-y<2,
系数化成1得y>-2. .
.
点评 本题考查了不等式与不等式组的解集,用数轴表示不等式的解集时,要注意“两定”:一是定界点,一般在数轴上只标出原点和界点即可.定边界点时要注意,点是实心还是空心,若边界点含于解集为实心点,不含于解集即为空心点;二是定方向,定方向的原则是:“小于向左,大于向右”.


科目:初中数学 来源: 题型:解答题
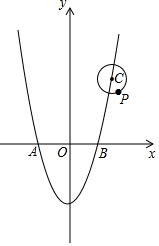 【材料阅读】阅读下列一段文字,然后回答下列问题.
【材料阅读】阅读下列一段文字,然后回答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
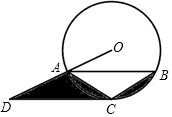 如图,△ABC内接于⊙O,CA=CB,CD∥AB且与OA的延长线交于点D.
如图,△ABC内接于⊙O,CA=CB,CD∥AB且与OA的延长线交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
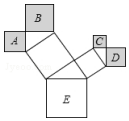 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、E的面积分别为2,5,1,10.则正方形D的面积是2.
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、E的面积分别为2,5,1,10.则正方形D的面积是2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.2 | B. | 0.25 | C. | 0.4 | D. | 0.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
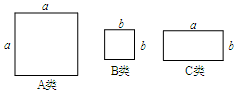
| A. | a+2b | B. | 2a+b | C. | 2a+2b | D. | a+b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省襄阳市九年级下学期第一次月考数学试卷(解析版) 题型:单选题
一个圆形人工湖如图所示,弦AB是湖上的一座桥,已知桥AB长100m,测得圆周角∠ACB=45°,则这个人工湖的直径AD为( )

A. 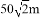 B.
B. 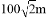 C.
C. 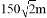 D.
D. 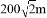
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com