
 【材料阅读】阅读下列一段文字,然后回答下列问题.
【材料阅读】阅读下列一段文字,然后回答下列问题.分析 (1)依据两点间的距离公式可求得AB的长;
(2)依据两点间的距离公式可求得AB、AC、BC的长,然后依据勾股定理的逆定理可对△ABC的形状作出判断;
(3)①令y=0得:x2-4=0,解得x=2或x=-2,故此可得到A,B的坐标;②首先依据两点间的距离公式表示出PA2+PB2的长,通过化简可得到PA2+PB2=2PO2+8,然后求得OP的最大值,从而可得到问题的答案.
解答 解:(1)AB=$\sqrt{[2-(-4)]^{2}+(-3-5)^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10.
(2)AB2=(-1-0)2+(2-4)2=1+4=5;
AC2=(0-4)2+(4-2)2=16+4=20;BC2=(-1-4)2+(2-2)2=25,
∴BC2=AB2+AC2.
∴△ABC为直角三角形.
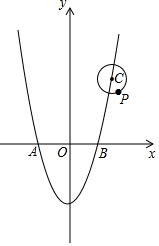
(3)①令y=0得:x2-4=0,解得x=2或x=-2,
∴A(-2,0),B(2,0).
②PA2+PB2=(m+2)2+n2+(m-2)2+n2=2(m2+n2)+8=2PO2+8.
当OP过圆心C时,PO最大,最大值=OC+PC=5+1=6.
因此PA2+PB2最大值为2×62+8=80.
点评 本题主要考查的是二次函数的综合、两点间的距离公式,依据两点间的距离公式得到PA2+PB2=2PO2+8是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2 | B. | y1>y2 | ||
| C. | y1=y2 | D. | y1、y2、的大小不确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
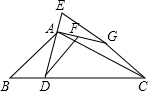 如图,在△ABC中,∠B=45°,∠ACB=30°,点D是BC上一点,连接AD,过点A作AG⊥AD,点F在线段AG上,延长DA至点E,使AE=AF,连接EG,CG,DF,若EG=DF,点G在AC的垂直平分线上,则$\frac{AB}{CG}$的值为$\frac{\sqrt{3}+1}{2}$.
如图,在△ABC中,∠B=45°,∠ACB=30°,点D是BC上一点,连接AD,过点A作AG⊥AD,点F在线段AG上,延长DA至点E,使AE=AF,连接EG,CG,DF,若EG=DF,点G在AC的垂直平分线上,则$\frac{AB}{CG}$的值为$\frac{\sqrt{3}+1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com