
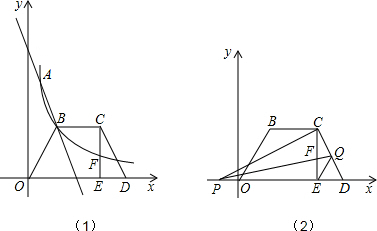
���� ��1����A����뷴������������ʽ�����k2����B���������a��ֵ���ٰ�A��B�����������һ�κ�������ʽ�����k1��
��2����B��BG��x���ڵ�G����B����������BG��OG�����ɵ������ε����ʿ�֤����BOG�ա�CDE�������ε���������EG�ij���������C�����꣬�����F������꣬����˫���߽���ʽ�����EF�ij�����֤��FC=EF��
��3����������֤����CED�ס�PCD�������PD�ij���������P�����꣬��Q��QH��x���ڵ�H�������QH�������á�QDE�͡�PCD������������S1��S2��ֵ���������ֵ��
��� �⣺��1���߷���������y=$\frac{{k}_{2}}{x}$��ͼ�����A��1��6����B��a��3�����㣬
��6=$\frac{{k}_{2}}{1}$�����k2=6��
��3a=6�����a=2��
��B��2��3����
��ֱ��y=k1 x+b��A��B���㣬
���A��B�������ɵ�$\left\{\begin{array}{l}{6={k}_{1}+b}\\{3=2{k}_{1}+b}\end{array}\right.$�����$\left\{\begin{array}{l}{{k}_{1}=-3}\\{b=9}\end{array}\right.$��
���Ͽ�֪k1=-3��k2=6��
��2��FC=EF���������£�
��ͼ1����B��BG��x���ڵ�G��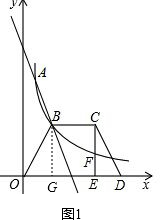
��B��2��3����
��OG=2��BG=3��
��BC��OD��OB=CD��
���BOG=��CDE��
�ڡ�BOG�͡�CDE�У�
$\left\{\begin{array}{l}{��BOG=��CDE}\\{��BGO=��CED}\\{OB=CD}\end{array}\right.$��
���BOG�ա�CDE��AAS����
��OG=DE=2��CE=BG=3��
��S����OBCD=12��
��$\frac{1}{2}$��OD+BC��•CE=12������2��2+BC+BC����3=24��
��BC=2��
��OE=OG+GE=2+2=4��
��F�������Ϊ4��
��F��˫�����ϣ����ɣ�1����֪˫���߽���ʽΪy=$\frac{6}{x}$��
��y=$\frac{6}{4}$=$\frac{3}{2}$��
��EF=$\frac{3}{2}$����FC=CE-EF=3-$\frac{3}{2}$=$\frac{3}{2}$��
��FC=EF��
��3����Rt��CED��ED=2��CE=3��
��CD=$\sqrt{C{E}^{2}+E{D}^{2}}$=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$��
����PCD=90��ʱ�����CED=��PCD���ҡ�CDE=��PDC��
���CED�ס�PCD��
��$\frac{CD}{PD}$=$\frac{DE}{CD}$����$\frac{\sqrt{13}}{PD}$=$\frac{2}{\sqrt{13}}$�����PD=$\frac{13}{2}$��
��OP=PD-OD=$\frac{13}{2}$-6=$\frac{1}{2}$��
��P��������-$\frac{1}{2}$��0����
��ͼ2����Q��QH�ɣ�2��֪FΪCE�е㣬��QΪCD�е㣬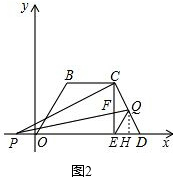
��HΪDE�е㣬
��QH=$\frac{1}{2}$CE=$\frac{3}{2}$��
��S2=S��QDE=$\frac{1}{2}$DE•QH=$\frac{1}{2}$��2��$\frac{3}{2}$=$\frac{3}{2}$��S��PDC=$\frac{1}{2}$PD•CE=$\frac{1}{2}$��$\frac{13}{2}$��3=$\frac{39}{4}$��
��S1=S�ı���PCQE=S��PDC-S��QDE=S��PDC=$\frac{39}{4}$-$\frac{3}{2}$=$\frac{33}{4}$��
��S1��S2=$\frac{33}{4}$��$\frac{3}{2}$=11��2��
���� ������Ҫ���鷴�����������ۺ�Ӧ�ã��漰����ϵ������ȫ�������Ρ����������ε��ж������ʡ��������ε����ʵ�֪ʶ�㣮�ڣ�1�����ս���������������������ʽ�ǽ���Ĺؼ����ڣ�2�������F��ĺ������ǽ���Ĺؼ����ڣ�3�������PD���ǽ���Ĺؼ���ע�����������߶�����Ӧ�ã����⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�


 �ٷ�ѧ����ҵ��������ϵ�д�
�ٷ�ѧ����ҵ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
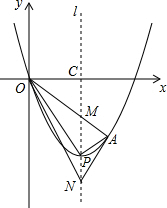 ��ͼ������ΪP��2��-4���Ķ��κ���ͼ��ԭ�㣨0��0������A�ڸ�ͼ���ϣ�OA����Գ���l�ڵ�M��
��ͼ������ΪP��2��-4���Ķ��κ���ͼ��ԭ�㣨0��0������A�ڸ�ͼ���ϣ�OA����Գ���l�ڵ�M���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0�� | B�� | 1�� | C�� | 2�� | D�� | 3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���߶�AB��CD�ֱ���һ���γ���һ���ͳ�����ʻ�����������ڵ�ʣ������y1��������y2������������ʻʱ��x��Сʱ���ĺ���ͼ��
��ͼ���߶�AB��CD�ֱ���һ���γ���һ���ͳ�����ʻ�����������ڵ�ʣ������y1��������y2������������ʻʱ��x��Сʱ���ĺ���ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 20 | B�� | 19.5 | C�� | 14.5 | D�� | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
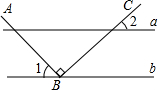 ��ͼ��ʾ��ֱ��a��b����B��ֱ��b�ϣ���AB��BC����1=55�㣬���2�Ķ���Ϊ��������
��ͼ��ʾ��ֱ��a��b����B��ֱ��b�ϣ���AB��BC����1=55�㣬���2�Ķ���Ϊ��������| A�� | 55�� | B�� | 45�� | C�� | 35�� | D�� | 25�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com