
分析 设抛物线解析式为y=ax2+bx+c,抛物线与x轴两交点坐标为(x1,0),(x2,0),且x2>x1,根据题意列出方程组,求出方程组的解得到a,b,c的值,即可确定出解析式.
解答 解:设抛物线解析式为y=ax2+bx+c,抛物线与x轴两交点坐标为(x1,0),(x2,0),且x2>x1,
根据题意得:$\left\{\begin{array}{l}{a+b+c=6}\\{a-b+c=-2}\\{{x}_{2}-{x}_{1=2\sqrt{7}}}\end{array}\right.$,且|x2-x1|=|$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$-$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$|=2$\sqrt{7}$,
解得a=-$\frac{1}{3}$,b=4,c=2$\frac{1}{3}$或a=1,b=4,c=1,
所以此抛物线解析式是-$\frac{1}{3}$x2+4x+2$\frac{1}{3}$或y=x2+4x+1.
点评 此题考查了待定系数法求二次函数解析式,熟练掌握待定系数法是解本题的关键.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
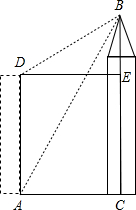 小强的家在某公寓楼AD内,他家的前面新建了一座大厦BC,小强想知道大厦的高度,但由于施工原因,无法测出公寓底部A与大厦底部C的直线距离.于是小强在他家的楼底A处测得大厦顶部B的仰角为60°,爬上楼顶D处测得大厦的顶部B的仰角为30°.已知公寓楼AD的高为30m,请你帮助小强计算出大厦BC的高度.
小强的家在某公寓楼AD内,他家的前面新建了一座大厦BC,小强想知道大厦的高度,但由于施工原因,无法测出公寓底部A与大厦底部C的直线距离.于是小强在他家的楼底A处测得大厦顶部B的仰角为60°,爬上楼顶D处测得大厦的顶部B的仰角为30°.已知公寓楼AD的高为30m,请你帮助小强计算出大厦BC的高度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△OAB中,∠ABO=90°,∠AOB=30°,将△AOB绕点O逆时针方向旋转95°得到△OA1B1,则∠A1OB的度数为65°.
如图,在△OAB中,∠ABO=90°,∠AOB=30°,将△AOB绕点O逆时针方向旋转95°得到△OA1B1,则∠A1OB的度数为65°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
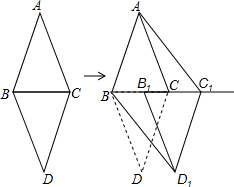 如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=3cm.BC=2cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1,连接AC1,BD1.如果四边形ABD1C1是矩形,那么平移的距离为7cm.
如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=3cm.BC=2cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1,连接AC1,BD1.如果四边形ABD1C1是矩形,那么平移的距离为7cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$-3$\sqrt{2}$=$\sqrt{2}$ | B. | |$\sqrt{3}$-1.7|=1.7-$\sqrt{3}$ | C. | $\sqrt{\frac{4}{9}}$=±$\frac{2}{3}$ | D. | $\root{3}{-1}$=-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com