
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 ①根据$\frac{a+1}{a-1}≠-1$,可得结论①不正确,据此判断即可.
②根据$\frac{{(a-b)}^{2}}{{(b-a)}^{2}}=1$,可得结论②不正确,据此判断即可.
③根据分式的基本性质,可得$\frac{6-2x}{-x+3}=2$,所以结论③正确,据此判断即可.
④根据$\frac{{x}^{2}{+y}^{2}}{x+y}≠x+y$,可得结论④不正确,据此判断即可.
解答 解:∵$\frac{a+1}{a-1}≠-1$,
∴结论①不正确;
∵$\frac{{(a-b)}^{2}}{{(b-a)}^{2}}=1$,
∴结论②不正确;
∵$\frac{6-2x}{-x+3}=2$,
∴结论③正确;
∵$\frac{{x}^{2}{+y}^{2}}{x+y}≠x+y$,
∴结论④不正确.
综上,可得
计算正确的有1个:③.
故选:B.
点评 此题主要考查了分式的基本性质的应用,要熟练掌握,解答此题的关键是要明确:分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变.


科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
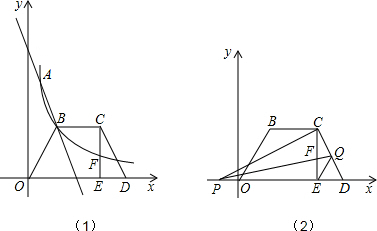
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
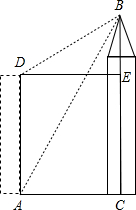 小强的家在某公寓楼AD内,他家的前面新建了一座大厦BC,小强想知道大厦的高度,但由于施工原因,无法测出公寓底部A与大厦底部C的直线距离.于是小强在他家的楼底A处测得大厦顶部B的仰角为60°,爬上楼顶D处测得大厦的顶部B的仰角为30°.已知公寓楼AD的高为30m,请你帮助小强计算出大厦BC的高度.
小强的家在某公寓楼AD内,他家的前面新建了一座大厦BC,小强想知道大厦的高度,但由于施工原因,无法测出公寓底部A与大厦底部C的直线距离.于是小强在他家的楼底A处测得大厦顶部B的仰角为60°,爬上楼顶D处测得大厦的顶部B的仰角为30°.已知公寓楼AD的高为30m,请你帮助小强计算出大厦BC的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com