
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��A������Ϊ����8��0������B������Ϊ����8��6����ֱ��BC��x�ᣬ��y���ڵ�C�����ı���OABC�Ƶ�O��˳ʱ�뷽����ת���ȵõ��ı���OA��B��C�䣬��ʱֱ��OA�䡢ֱ��B��C��ֱ���ֱ��BC�ཻ�ڵ�P��Q��
��1���ı���OABC����״�� �� ����=90��ʱ�� ![]() ��ֵ�� ��
��ֵ�� ��
��2������ͼ2�����ı���OA��B��C��Ķ���B������y����������ʱ���� ![]() ��ֵ��
��ֵ��
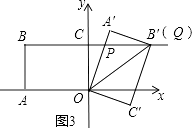
����ͼ3�����ı���OA��B��C��Ķ���B������BC���ӳ�����ʱ�����OPB��������

��3�����ı���OABC��ת�����У���0�㣼����180��ʱ���Ƿ���������ĵ�P�͵�Q��ʹBP= ![]() BQ�������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
BQ�������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1������![]()
��2��
�⣺��ͼ2��
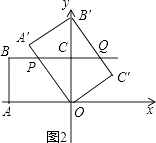
�ߡ�POC=��B��OA�䣬��PCO=��OA��B��=90�㣬
���COP�ס�A��OB�䣮
�� ![]() ����
���� ![]() ��
��
��CP= ![]() ��BP=BC��CP=
��BP=BC��CP= ![]() ��
��
ͬ����B��CQ�ס�B��C��O��
�� ![]() ��
��
�� ![]()
��CQ=3��BQ=BC+CQ=11��
�� 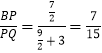 ��
��
�� ![]() ��
��
��ͼ3���ڡ�OCP�͡�B��A��P�У� 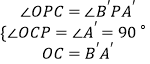 ��
��
���OCP�ա�B��A��P��AAS����
��OP=B��P��
��B��P=x��
��Rt��OCP����8��x��2+62=x2��
���x= ![]() ��
��
��S��OPB��= ![]() ��
�� ![]() ��6=
��6= ![]()
��3��
�⣺���������ĵ�P�͵�Q��ʹBP= ![]() BQ��
BQ��
��P��������P1����9�� ![]() ��6����P2����
��6����P2���� ![]() ��6����
��6����
���ɣ�
����Q��QH��OA����H������OQ����QH=OC��=OC��
��S��POQ= ![]() PQOC��S��POQ=
PQOC��S��POQ= ![]() OPQH��
OPQH��
��PQ=OP��
��BP=x��
��BP= ![]() BQ��
BQ��
��BQ=2x��
��ͼ4������P�ڵ�B���ʱ��
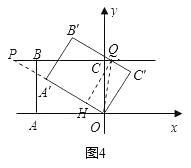
OP=PQ=BQ+BP=3x��
��Rt��PCO����8+x��2+62=��3x��/span>2��
���x1=1+ ![]() ��x2=1��
��x2=1�� ![]() ������ʵ�ʣ���ȥ����
������ʵ�ʣ���ȥ����
��PC=BC+BP=9+ ![]() ��
��
��P����9�� ![]() ��6����
��6����
��ͼ5������P�ڵ�B�Ҳ�ʱ��
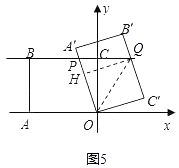
��OP=PQ=BQ��BP=x��PC=8��x��
��Rt��PCO����8��x��2+62=x2�����x= ![]() ��
��
��PC=BC��BP=8�� ![]() =
= ![]() ��
��
��P���� ![]() ��6����
��6����
���Ͽ�֪�����ڵ�P����9�� ![]() ��6����
��6���� ![]() ��6����ʹBP=
��6����ʹBP= ![]() BQ��
BQ��
���������⣺��1��ͼ1���ı���OA��B��C�����״�Ǿ��Σ�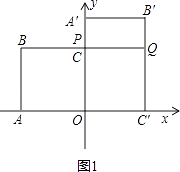
�ߵ�A������Ϊ����8��0������B����8��6����
��AB��OC��
��BC��x�ᣬ
���ı���OABC��ƽ���ı��Σ�
��OC��OA��
��ƽ���ı���OABC����״�Ǿ��Σ�
����=90��ʱ��P��C�غϣ���ͼ1��
BP=8��BQ=BP+OC=8+6=14��
�� ![]() ��
��
���Ǿ��εij�����ıȣ��� ![]() ��
��
���Դ��Ǿ��Σ� ![]() ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC���A��B��C�䶼�ǵ��������Σ���AB=AC=5��A��B��=A��C��=3������B+��B��=90�㣬���ABC���A��B��C��������Ϊ 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����߳�Ϊ3�������εĶԽ��߳�Ϊa�����й���a������˵����
��a����������
��a�����������ϵ�һ��������ʾ��
��3��a��4��
��a��18������ƽ������
���У�������ȷ˵��������ǣ� ��
A.�٢�
B.�ڢ�
C.�٢ڢ�
D.�٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y1=x2+mx+n��ͼ����P����3��1�����Գ����Ǿ�������1��0����ƽ����y���ֱ�ߣ�
��1����m��n��ֵ��
��2����ͼ��һ�κ���y2=kx+b��ͼ����P����x���ཻ�ڵ�A������κ�����ͼ���ཻ����һ��B����B�ڵ�P���Ҳ࣬PA��PB=1��5����һ�κ����ı���ʽ�� 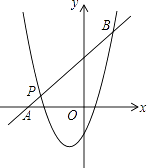
��3��ֱ��д��y1��y2ʱx��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���������ߣ��ں��߲���λ�����������С���߶�AC����ͼ��ʾ�������ڵ�B���ɽ����A������Ϊ30�㣬Ȼ������������ǰ��62�ף�����D�㣬�ڲ��ɽ����A������Ϊ60�㣨B��C��D������ͬһˮƽ���ϣ��Ҳ����ǵĸ߶Ⱥ��Բ��ƣ�����С���߶�AC�������ȷ��1�ף��ο���ֵ�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�D��BC���ϵ�һ�㣬E��AD���е㣬��A����BC��ƽ���߽�CE���ӳ�����F����AF=BD������BF�� 
��1����֤��D��BC���е㣮
��2�����AB=AC�����ж��ı���AFBD����״����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O�����ߣ��е�ΪB������AO��AO���O���ڵ�C��BDΪ��O��ֱ��������CD������A=30�㣬��O�İ뾶Ϊ2����ͼ����Ӱ���ֵ����Ϊ��������
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ǿѧ��������ʶ��ij��ѧ��֯ȫУ2000��ѧ���μӻ���֪ʶ�����������ɼ���Ϊ���������г�ȡ����ͬѧ�ijɼ�����ͳ�ƣ������Ƴ���ͼͳ��ͼ�������ͼ���ṩ����Ϣ������������⣺
��1������ȡ�ijɼ�������ͼ�����������ʾ�������飨79.5��89.5���������ε�Բ�Ľ�Ϊ ��
��2�����ɼ���90�����ϣ���90�֣���ͬѧ���Ի�����Ƹ�УԼ�ж�����ͬѧ��
��3��ij�����ӳɼ���õ�4��ͬѧ���С�Ů��2���������ѡȡ2��ͬѧȥ�������л�����������ѡ����ͬѧǡ����1��1Ů�ĸ���Ϊ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣��뾶ΪR��Բ�Ľ�Ϊn������������S����=![]() ���ɻ���l=
���ɻ���l=![]() ����S����=
����S����=![]() =
=![]()
![]() R=
R=![]() lR��ͨ���۲죬���Ƿ���S����=
lR��ͨ���۲죬���Ƿ���S����=![]() lR������S������=
lR������S������=![]() ���ס��ߣ�
���ס��ߣ�
������Σ�����̽���Ȼ�����ͼ�ڣ�����ͬ��ԲΧ�ɵ�Բ�������νصõ�һ���ֽ����Ȼ����������ʽ����Ӧ�ã�
��1�����Ȼ������ΪS�Ȼ� �� ![]() �ij�Ϊl1 ��
�ij�Ϊl1 �� ![]() �ij�Ϊl2 �� �߶�AD�ij�Ϊh��������ͬ��Բ�뾶R��r�IJ�����S����=
�ij�Ϊl2 �� �߶�AD�ij�Ϊh��������ͬ��Բ�뾶R��r�IJ�����S����=![]() �����ϵ�+�µף����ߣ��ú�l1 �� l2 �� h�Ĵ���ʽ��ʾS�Ȼ� �� ��֤����
�����ϵ�+�µף����ߣ��ú�l1 �� l2 �� h�Ĵ���ʽ��ʾS�Ȼ� �� ��֤����
��2����һ�γ�Ϊ40m�����Χ��һ����ͼ����ʾ���Ȼ��λ����߶�AD�ij�hΪ����ʱ�������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com