
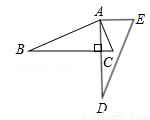
如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,若∠CAE=55°,∠E=70°,且AD⊥BC,则∠BAC的度数为 .
85°.
【解析】
试题分析:由题意得:∠BAC=∠DAE,∠D=∠B,∴∠BAD=∠CAE=65°,∵AD⊥BC,∴∠B=90°﹣∠BAC=25°,∠D=25°,∴∠DAE=180°﹣25°﹣70°=85°,∴∠BAC=85°,故答案为:85°.
考点:旋转的性质.
考点分析: 考点1:图形的平移与旋转 定义:

科目:初中数学 来源:2014-2015学年江苏省东台市九年级下学期第一次质量检测数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系中,抛物线y=ax 2+bx+4经过A(-3,0)、B(4,0)两点,且与y轴交于点C,D(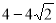 ,0).动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时动点Q从点C出发,沿线段CA以某一速度向点A移动.
,0).动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时动点Q从点C出发,沿线段CA以某一速度向点A移动.
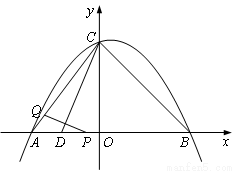
(1)求该抛物线的解析式;
(2)若经过t秒的移动,线段PQ被CD垂直平分,求此时t的值;
(3)在第一象限的抛物线上取一点G,使得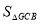 =
=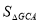 ,再在抛物线上找点E(不与点A、B、C重合),使得∠GBE=45°,求E点的坐标.
,再在抛物线上找点E(不与点A、B、C重合),使得∠GBE=45°,求E点的坐标.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省大庆市九年级上学期期末检测数学试卷(解析版) 题型:解答题
(8分)如图,在△ABC中,D是BC的垂直平分线DH上一点,DF⊥AB于F,DE⊥AC交AC的延长线于E,且BF=CE.
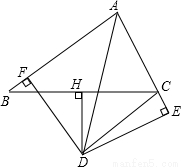
(1)求证:AD平分∠BAC;
(2)若∠BAC=80°,求∠DCB的度数.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省大庆市九年级上学期期末检测数学试卷(解析版) 题型:填空题
在□ABCD的周长为22厘米,两条对角线相交于点O,三角形AOB的周长比三角形BOC的周长大5厘米,则AD=________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省大庆市九年级上学期期末检测数学试卷(解析版) 题型:选择题
在□ABCD中, ∠A:∠B:∠C:∠D可以是( )
A.1:2:2:1 B.2:1:1:2 C.2:2:1:1 D.2:3:2:3
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省大庆市九年级上学期期末检测数学试卷(解析版) 题型:选择题
如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
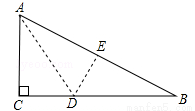
A.2cm B.3cm C.4cm D.5cm
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省邯郸市九年级第一次模拟考试数学试卷(解析版) 题型:选择题
某篮球队12名队员的年龄如下表所示:
年龄(岁) | 18 | 19 | 20 | 21 |
人数 | 5 | 4 | 1 | 2 |
则这12名队员年龄的众数和中位数分别是( )
A.18,19 B.18,19.5 C.5,4 D.5, 4.5
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省台州市九年级上学期第一次月考数学试卷(解析版) 题型:解答题
已知关于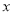 的一元二次方程
的一元二次方程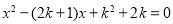 的两个实数根为
的两个实数根为 ,
,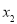 .
.
(1)求k的取值范围。
(2)是否存在实数可k,使得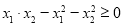 成立?若存在,请求出k值,若不存在,请说明理由.
成立?若存在,请求出k值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com