
已知关于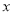 的一元二次方程
的一元二次方程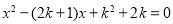 的两个实数根为
的两个实数根为 ,
,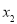 .
.
(1)求k的取值范围。
(2)是否存在实数可k,使得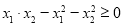 成立?若存在,请求出k值,若不存在,请说明理由.
成立?若存在,请求出k值,若不存在,请说明理由.
(1)k≤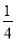 ;
;
(2)存在实数k使得x1·x2-x12-x22≥0成立;理由见解析;
【解析】
试题分析:(1)由题意可得△≥0,即[﹣(2k+1)]2﹣4(k2+2k)≥0,通过解该不等式即可求得k的取值范围;
(2)假设存在实数k使得x1·x2-x12-x22≥0成立.由根与系数的关系可得x1+x2=2k+1,x1·x2=k2+2k,然后利用完全平方公式可以把x1·x2-x12-x22≥0转化为3x1·x2-(x1+x2)2≥0的形式,通过解不等式可以求得k的值.
试题解析:(1)∵原方程有两个实数根,
∴△≥0
即[﹣(2k+1)]2﹣4(k2+2k)≥0,
∴4k2+4k+1﹣4k2﹣8k≥0 ,
∴1﹣4k≥0,
∴k≤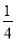 ,
,
∴当k≤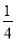 时,原方程有两个实数根;
时,原方程有两个实数根;
(2)假设存在实数k使得x1·x2-x12-x22≥0成立,
∵x1,x2是原方程的两根,
∴x1+x2=2k+1,x1·x2=k2+2k,
由x1·x2-x12-x22≥0,
得3x1·x2-(x1+x2)2≥0
∴3(k2+2k)﹣(2k+1)2≥0,
整理得:﹣(k﹣1)2≥0,
∴只有当k=1时,上式才能成立;
又∵由(1)知k≤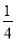 ,
,
∴不存在实数k使得x1·x2-x12-x22≥0成立;
考点:1、根与系数的关系;2、根的判别式
考点分析: 考点1:一元二次方程 定义:


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源:2014-2015学年黑龙江省大庆市九年级上学期期末检测数学试卷(解析版) 题型:填空题
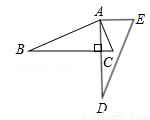
如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,若∠CAE=55°,∠E=70°,且AD⊥BC,则∠BAC的度数为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省武夷山市九年级上学期期末质量监测数学试卷(解析版) 题型:解答题
(12分)如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的矩形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至CE′F′D,旋转角为 .
.

(1)当点D′恰好落在EF边上时,则旋转角α的值为________度;
(2)如图2,G为BC中点,且0°<α<90°,求证:GD′=E′D;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,是否存在旋转角α,使△DCD′与△CBD′全等?若能,直接写出旋转角α的值;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省武夷山市九年级上学期期末质量监测数学试卷(解析版) 题型:选择题
如图,四边形ABCD是⊙O的内接四边形,若∠B=110o,则∠ADE的度数为( )

A.55 o B.70 o C.90 o D.110 o
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省武夷山市九年级上学期期末质量监测数学试卷(解析版) 题型:选择题
已知 是一元二次方程
是一元二次方程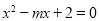 的一个解,则
的一个解,则 的值是( )
的值是( )
A.-3 B.3 C.0 D.0或3
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省台州市九年级上学期第一次月考数学试卷(解析版) 题型:填空题
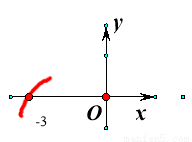
如图是抛物线y=ax2+2ax+2图象的一部分,(-3,0)是图象与x轴的一个交点,则不等式ax2+2ax+2>0的解集是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省台州市九年级上学期第一次月考数学试卷(解析版) 题型:选择题
把抛物线y=x2+bx+c的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式为y=x2-3x+5,则 ( ).
A.b=3,c=7 B.b=6,c=3
C.b=-9,c=-5 D.b=-9,c=21
查看答案和解析>>
科目:初中数学 来源:2014-2015学年云南省九年级上学期第一次月考数学试卷(解析版) 题型:填空题
用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地板,第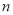 个图形中需要黑色瓷砖__________块(用含
个图形中需要黑色瓷砖__________块(用含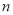 的代数式表示).
的代数式表示).

查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级上学期第一次月考数学试卷(解析版) 题型:解答题
(6分)在开展“雪雷锋社会实践”活动中,某校为了了解全校1200名学生参加活动的情况,随机调查了50名学生参加活动的次数,并根据数据绘成条形统计图(如图)
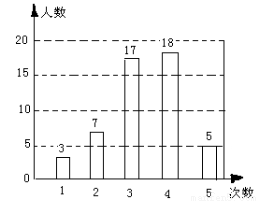
(1)求这50个样本数据的平均数、众数和中位数;
(2)根据样本数据,估计该校1200名学生共参加了多少次活动?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com