
��12�֣���ͼ1��ʾ����һ���߳�Ϊ2��������ABCD��һ����Ϊ2����Ϊ1�ľ���CEFDƴ��һ�𣬹���һ����ij�����ABEF���ֽ�С������CEFD�Ƶ�C˳ʱ����ת��CE��F��D����ת��Ϊ ��
��

��1������D��ǡ������EF����ʱ������ת�Ǧ���ֵΪ________�ȣ�
��2����ͼ2��GΪBC�е㣬��0�㣼����90�㣬��֤��GD��=E��D��
��3��С������CEFD�Ƶ�C˳ʱ����תһ�ܵĹ����У��Ƿ������ת�Ǧ���ʹ��DCD�����CBD��ȫ�ȣ����ܣ�ֱ��д����ת�Ǧ���ֵ�������ܣ�˵�����ɣ�
��1��30����2��֤���������������3���ܣ�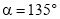 ��
��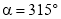 ��
��
��������
�����������1��������ת�����ʵõ�CD��ij�����Rt��CED���У�CD��=2��CE=1���õ���CD��E=30�㣬Ȼ�����ƽ���ߵ����ʼ��ɵõ��Ϧ��Ķ�����
��2����GΪBC�е�ɵ�CG=CE���ٸ�����ת�����ʵá�D��CE��=��DCE=90�㣬CE=CE��=CG�����GCD��=��DCE��=90��+�����ٸ��ݡ�SAS�����жϡ�GCD��ա�E��CD���õ�GD��=E��D��
��3�����������ε����ʵ�CB=CD����CD=CD�䣬���BCD�����DCD��Ϊ����ȵ������������Σ������������ʱ����ȫ�ȣ�����BCD�����DCD��Ϊ�۽�������ʱ���ɼ������=135�㣬����BCD�����DCD��Ϊ���������ʱ���ɼ���õ���=315�㣮
�����������1���߳�����CEFD�Ƶ�C˳ʱ����ת��CE��F��D�䣬��CD��=CD=2����Rt��CED���У�CD��=2��CE=1�����CD��E=30�㣬��CD��EF����Ϧ�=30�㣻
��2����GΪBC�е㣬��CG=1����CG=CE���߳�����CEFD�Ƶ�C˳ʱ����ת��CE��F��D�䣬���D��CE��=��DCE=90�㣬CE=CE��=CG�����GCD��=��DCE��=90��+�����ڡ�GCD��͡�E��CD�У���CD��=CD����GCD��=��DCE�䣬CG=CE�䣬���GCD��ա�E��CD��SAS������GD��=E��D��
��3���ܣ��������£����ı���ABCDΪ�����Σ���CB=CD����CD��=CD�䣬���BCD�����DCD��Ϊ����ȵ������������Σ�����BCD��=��DCD��ʱ����BCD��ա�DCD�䣬����BCD�����DCD��Ϊ�۽�������ʱ������ת�Ǧ�=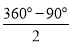 =135�㣬
=135�㣬
����BCD�����DCD��Ϊ���������ʱ����BCD��=��DCD��=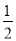 ��BCD=45�㣬���=360�㩁
��BCD=45�㣬���=360�㩁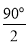 =315�㣬����ת��a��ֵΪ135���315��ʱ����BCD�����DCD��ȫ�ȣ�
=315�㣬����ת��a��ֵΪ135���315��ʱ����BCD�����DCD��ȫ�ȣ�
���㣺1����ת�����ʣ�2��ȫ�������ε��ж������ʣ�3�����ε����ʣ�4�������ε����ʣ�
��������� ����1��ͼ�ε�ƽ������ת ���壺


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014-2015ѧ�������ʡ�����о��꼶��ѧ����ĩ�����ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ����һ��ֱ��������ֽƬ����ֱ�DZ�AC=6cm��BC=8cm���ֽ�ֱ�DZ�AC��ֱ��AD�۵���ʹ������б��AB�ϣ�����AE�غϣ���CD���ڣ� ��
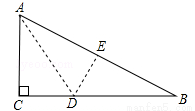
A��2cm B��3cm C��4cm D��5cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ��ӱ�ʡ�����о��꼶��һ��ģ�⿼����ѧ�Ծ��������棩 ���ͣ�ѡ����
ij�����12����Ա���������±���ʾ��
���䣨�꣩ | 18 | 19 | 20 | 21 |
���� | 5 | 4 | 1 | 2 |
����12����Ա�������������λ���ֱ��ǣ� ��
A��18��19 B��18��19��5 C��5��4 D��5�� 4��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ��ӱ�ʡ�����о��꼶��һ��ģ�⿼����ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ��AB��CD��EF��AB�ڵ�E��EF��CD�ڵ�F����֪��1=60�㣬���2�Ķ���Ϊ�� ��

A��20�� B��60�� C��30�� D��45��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�긣��ʡ����ɽ�о��꼶��ѧ����ĩ���������ѧ�Ծ��������棩 ���ͣ������
��8�֣���ͼ1��������ABCD��һ��6��6�����������ʾ��ͼ������ÿ��С�����εı߳�Ϊ1��λ��AD�е㴦�Ĺ��P��ͼ-2�ij����ƶ���
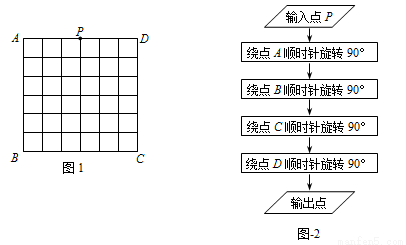
��1������ͼ-1�л������P������·����
��2������P������·���ܳ�����������У���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�긣��ʡ����ɽ�о��꼶��ѧ����ĩ���������ѧ�Ծ��������棩 ���ͣ������
��֪���κ���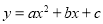 �У�����
�У�����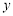 ���Ա���
���Ա���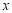 �IJ��ֶ�Ӧֵ���±���
�IJ��ֶ�Ӧֵ���±���
| �� | ��2 | ��1 | 0 | 1 | 2 | �� |
| �� | ��3 | ��4 | ��3 | 0 | 5 | �� |
��˶��κ����ĶԳ���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ���㽭ʡ̨���о��꼶��ѧ�ڵ�һ���¿���ѧ�Ծ��������棩 ���ͣ������
��֪����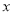 ��һԪ���η���
��һԪ���η���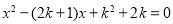 ������ʵ����Ϊ
������ʵ����Ϊ ��
��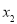 ��
��
��1����k��ȡֵ��Χ��
��2���Ƿ����ʵ����k,ʹ��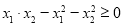 ����?������,�����kֵ,��������,��˵�����ɣ�
����?������,�����kֵ,��������,��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ������ʡ���꼶��ѧ�ڵ�һ���¿���ѧ�Ծ��������棩 ���ͣ�ѡ����
���䷽���ⷽ��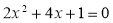 ���䷽��ķ����ǣ� ��
���䷽��ķ����ǣ� ��
A��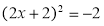 B��
B��
C�� D��
D��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com